今回はこちらの問題を解いていきます.
2次関数\(y=x^2\)のグラフと, 3次関数\(y=x^3+x^2-x-1\)のグラフの共通接線を求めよ. (2025 九州大学)
2次関数と3次関数の共通接線を求める問題です. 計算が少しだけハードで高次方程式も登場するので, 計算間違いがないかなど不安に駆られてしまう問題です. ここでは2つの解法を紹介しようと思います.
1つ目の解法は各関数のグラフで\(x\)座標が\(a\), \(b\)である点における接線をそれぞれ求めて, それらが一致する, つまり傾きと切片が一致するという条件のもと, \(a\), \(b\)の関係式を導出し, 求めるというものです.
2つ目の解法は3次関数のグラフで\(x\)座標が\(b\)である点における接線を求めて, その直線が2次間数のグラフに接するという条件から求めるものです. 「2次関数のグラフと直線(1次関数のグラフ)が接する」必要十分条件は, 「それらを連立して\(y\)を消去してできる\(x\)の2次方程式が重解を持つ」ということになります. これは教科書にも載っている有名事実なのでしっかり使えるようになりましょう.
なお, 問題を解く前にグラフを書いておくとこのようになります.
こういった問題では概形でも書いておくほうが, 求めた接線の妥当性を確認できるので良いかと思います.
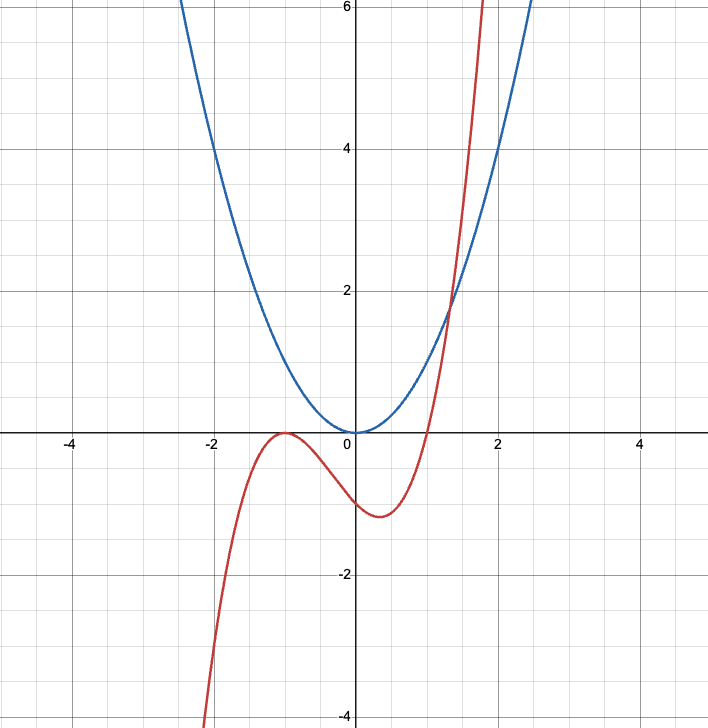
ではまずは1つ目の解法です.
\(y=x^2\), \(y=x^3+x^2-x-1\)をそれぞれ微分すると, \(y^\prime=2x\), \(y^\prime=3x^2+2x-x-1\)となるので, 各関数のグラフ上の点\((a,a^2)\), \((b,b^3+b^2-b-1)\)における接線はそれぞれ, \(y=2a(x-a)+a^2=2ax-a^2\), \(y=(3b^2+2b-1)(x-b)+b^3+b^2-b-1=(3b^2+2b-1)x-2b^3-b^2-1\)となる.
この2つの接線が一致するという条件から, 傾きと切片を比較して.
$$
\left\{ \begin{aligned}2a&=3b^2+2b-1\,\,\,\,\text{ ・・・①} \\ -a^2&=-2b^3-b^2-1\,\,\,\,\text{ ・・・②} \end{aligned} \right.
$$
を得る. ②を4倍すると,
$$
-4a^2=-8b^3-4b^2-4
$$
となり, 左辺\(-4a^2=-(2a)^2\)より, ①を代入すると,
$$
-(3b^2+2b-1)^2=-8b^3-4b^2-4
$$
とる. 展開して整理することで以下の\(b\)に関する4次方程式を得る.
$$
9b^4+4b^3-6b^2-4b-3=0
$$
この方程式は\(b=1\)とすると成り立つことがわかるので, 左辺の\(b\)の整式は\((b-1)\)で割り切れる. 割り算を実行することで,
$$
(b-1)(9b^3+13b^2+7b+3)=0
$$
を得る. ここで\(b\)の3次式\(9b^3+13b^2+7b+3\)は\(b=-1\)とすると\(0\)になることがわかるので, これはさらに\(b+1\)で割れる. 再び割り算を実行することで最終的に,
$$
(b-1)(b+1)(9b^2+4b+3)=0
$$
となる. \(b\)に関する2次方程式\(9b^2+4b+3=0\)は判別式が\(4^2-4\times 9 \times 3 <0\)となり実数解を持たないことがわかるので, この\(b\)の4次方程式の解は\(b=-1, 1\)の2つであることがわかる.
①から, \(b=-1\)のとき\(a=0\), \(b=1\)のとき\(a=2\)となり 求める共通接線は,
$$
y=0\,\,\mbox{と}\,\,y=4x-4
$$
の2つである.
次に2つ目の解法です.
\(y=x^3+x^2-x-1\)を微分すると, \(y^\prime=3x^2+2x-x-1\)となり, グラフ上の点\((b,b^3+b^2-b-1)\)における接線は\(y=(3b^2+2b-1)(x-b)+b^3+b^2-b-1=(3b^2+2b-1)x-2b^3-b^2-1\)となる.
この3次関数の接線が2次関数\(y=x^2\)に接する条件は, 2次関数と接線の方程式
$$
\left\{ \begin{aligned}y&=x^2 \\ y&=(3b^2+2b-1)x-2b^3-b^2-1\end{aligned} \right.
$$
から\(y\)を消去した\(x\)に関する2次方程式が重解を持つことである. \(y\)を消去すると,
$$
x^2=(3b^2+2b-1)x-2b^3-b^2-1
$$
となり, \(x\)に関して整理すると,
$$
x^2-(3b^2+2b-1)x+2b^3+b^2+1=0
$$
となり, これが重解を持つ必要十分条件は判別式が0になることで,
$$
\{-(3b^2+2b-1)\}^2-4\cdot 1\cdot (2b^3+b^2+1)=0
$$
である. 展開して整理すると,
$$
9b^4+4b^3-6b^2-4b-3=0
$$
となり, これは1つめの解法で得た\(b\)の4次方程式と一致するので, 同様にして, \(b=-1, 1\)が解であることがわかる. これから求める共通接線は,
$$
y=0\,\,\mbox{と}\,\,y=4x-4
$$
の2つである.
グラフを書いてみると確かに2本の直線が共通接線になっていることがわかります.
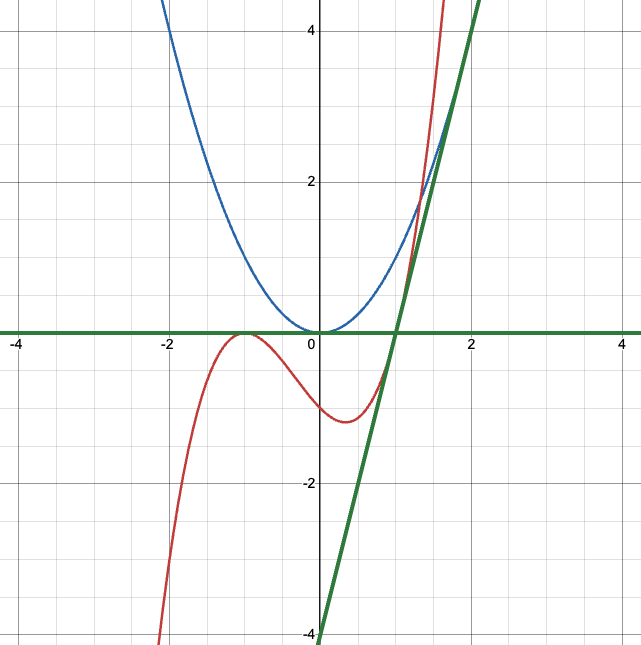
今回は\(b\)に関する条件式を愚直に展開して\(b\)の4次方程式を得ましたが, 各解法で少し工夫をすれば4次方程式を解かない方法もあります.
例えば解法1では\(-(3b^2+2b-1)^2=-8b^3-4b^2-4\)の条件式にて, \(b=-1\)とすることで両辺が\(0\)になることに気付けば, 展開前に両辺を\((b+1)\)でくくることが可能ですし, 解法2では\(\{-(3b^2+2b-1)\}^2-4\cdot 1\cdot (2b^3+b^2+1)=0\)の左辺の2つの項それぞれが\((b+1)\)でくくることが可能です. こちらの方が割り算が楽になる気はしますが, 本番の極限状態でこの事実に気づけるかはわかりませんし, 愚直に展開して\(b\)の値をいくつか代入して解く方が確実という考えもあるかと思いますのでなんとも言えません.
youtubeでも解説しています.
