【九州大学入試】2つの二次関数の共通接線と囲まれる面積(2024)

2025年7月11日

今回はこちらの問題を解いていきます.

次の2つの放物線
$$
C_1:y=2x^2,\,\,\, C_2:y=2x^2-8x+16
$$
の両方に接する直線$l$を求めよ. またその直線$l$と$C_1$, $C_2$で囲まれた領域の面積を求めよ.
(2024 九州大学文系[1])

こちら2次関数, 接線, 積分のとても基本的な問題です. 確実に点を取る必要があります.

それでは解いていきましょう.

$C_1$上の点$(a,2a^2)$で$C_1$に接する直線を求める. $y=2x^2$に関して, $y^\prime=4x$だから, $(a,2a^2)$における接線の傾きは$4a$である. この接線は$(a,2a^2)$を通ることから, その方程式は,
$$
\begin{align}
y-2a^2&=4a(x-a)\\
y&=4ax-2a^2
\end{align}
$$となる.

この接線が$C_2$にも接するときの$a$の値を求める. 直線が2次関数グラフ(放物線)と接する必要十分条件は, 2つの方程式から$y$を消去してできる, $x$の2次方程式が重解を持つことである.
$$
\left\{
\begin{array}{ll}
y = 4ax-2a^2 & \text{・・・①} \\
y=2x^2-8x+16 & \text{・・・②}
\end{array}
\right.
$$
①を②に代入して,
$$
\begin{align}
4ax-2a^2 = 2x^2-8x+16&\\
2x^2-(4a+8)x+2a^2+16&=0\\
x^2-2(a+2)x+a^2+8&=0 \text{・・・③}
\end{align}
$$となる. これが重解を持つ必要十分条件は, この2次方程式の判別式が0であることだから,
$$
\begin{align}
\frac{D}{4}=&\left\{-\left(a+2\right)\right\}^2-1\cdot\left(a^2+8\right)=0\\
&a^2+4a+4-a^2-8=0\\
&4a-4=0\\
&a=1
\end{align}
$$

よって直線$l$は, $y=4x-2$である.

このとき, $C_1$, $C_2$, $l$のグラフを書くと, 以下のようになる. ここで, $A$は$C_1$と$l$の, $B$は$C_2$と$l$の接点である.

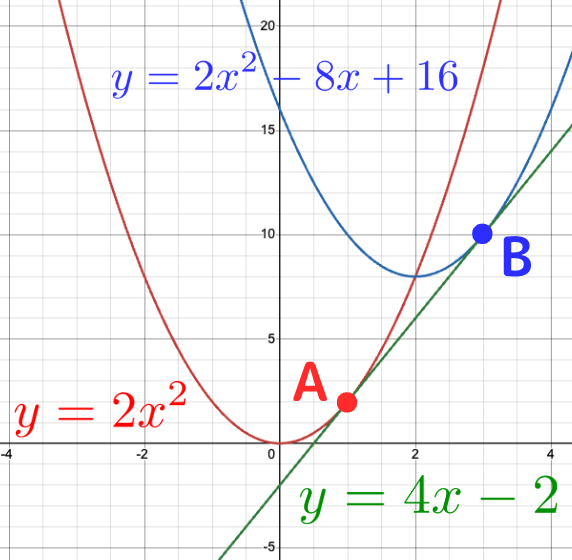
$a=1$から$A(1,2)$であることはすぐにわかる. $a=1$のとき, ③の2次方程式は,
$$
x^2-6x+9=0
$$となり, これは$(x-3)^2=0$から$x=3$, つまり, $B$の$x$座標は$3$である. これから$B(3,10)$であることがわかる.

$C_1$, $C_2$の方程式を連立して, 2つの曲線の交点$D$を求める.
$$
\left\{
\begin{array}{ll}
y = 2x^2 & \text{・・・④} \\
y=2x^2-8x+16 & \text{・・・⑤}
\end{array}
\right.
$$$y$を消去して計算すると,
$$
\begin{align}
2x^2&=2x^2-8x+16\\
8x&=16\\
x&=2
\end{align}
$$となる. さらに, $x=2$を$C_1$の方程式$y=2x^2$に代入すると$y=8$となるので, 交点$D$は$(2,8)$であることがわかる.

改めてグラフを書くと以下のようになっており, $1\leq x\leq 2$の範囲で$C_1$と$l$と直線$x=2$で囲まれた面積と, $2\leq x\leq 3$の範囲で$C_2$と$l$と直線$x=2$で囲まれた面積を求め, それを合計したものが\$C_1$, $C_2$, $l$で囲まれる面積となることがわかる.

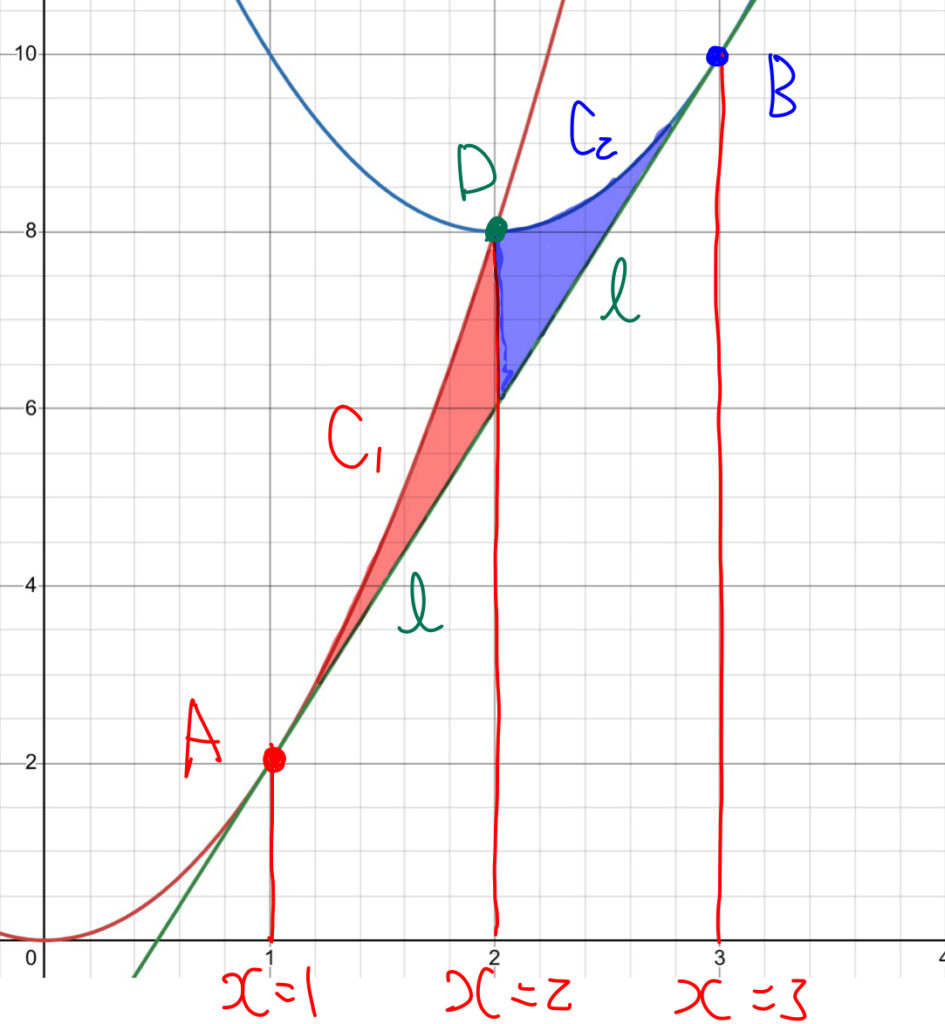
よって, 求める面積は,
$$
\begin{align}
&\int_1^2\left\{2x^2-(4x-2)\right\}dx+\int_2^3\left\{(2x^2-8x+16)-(4x-2)\right\}dx\\
&=\int_1^2\left(2x^2-4x+2\right)dx+\int_2^3\left(2x^2-12x+18\right)dx\\
&=\left[\frac{2}{3}x^3-2x^2+2x\right]_1^2+\left[\frac{2}{3}x^3-6x^2+18x\right]_2^3\\
&=\frac{16}{3}-8+4-\frac{2}{3}+2-2+18-54+54-\frac{16}{3}+24-36\\
&=\frac{4}{3}
\end{align}
$$となる.