今回はこちらの問題を解いていきます.
点Oを中心とする半径\(1\)の円周上に, 以下の3条件を満たすように4点A, B, C, Dをとる.
・点A, B, C, Dは円周上で反時計回りにこの順で並ぶ
・線分\(AD\)は円の直径
・\(AC=CD\)
・\(AB=BC\)
また, 線分\(AC\)と線分\(BD\)の交点をEとする. このとき, 以下の値をそれぞれ求めよ.
(1) \(\angle{ACB}\)
(2) \(BC\)
(3) 三角形\(BCE\)の面積
(2025 九州大学理系[4])
こちら問題文に図が与えられていない図形問題です. 条件から適切な図を書きましょう. 解答後に補足説明をしますが, 図はそれなりに綺麗に書くべきです. 図を書いたら辺の長さ, 角の大きさ, どの辺とどの辺の大きさが等しいか, どの角とどの角が等しいか, とにかく書きまくりましょう. そうすると閃くこともあるはずです.
それでは解いていきましょう.
(1) 与えられた条件から図を描くと以下となる.
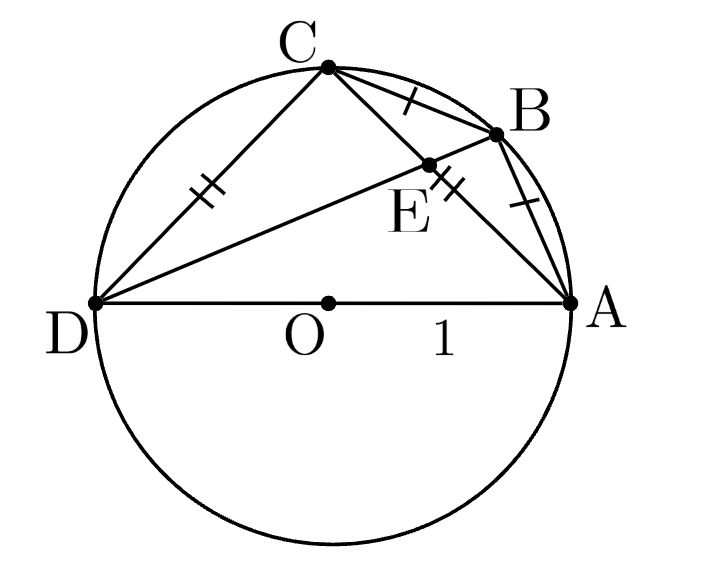
三角形\(ABC\)は\(AB=BC\)の二等辺三角形なので, その底角は等しく\(\angle{BAC}=\angle{BCA}\)である. 円周角の定理から\(\angle{BAC}=\angle{BDC}\), \(\angle{BCA}=\angle{ADB}\)となるので, 4つの角\(\angle{BAC}\), \(\angle{BCA}\), \(\angle{ADB}\), \(\angle{BDC}\)はいずれも等しい.
また, ADは円の直径であるから, \(\angle{ACD}=\frac{\pi}{2}\)であり, \(AC=CD\)であるから三角形\(ACD\)は\(\angle{ACD}\)が直角となる直角二等辺三角形である. よって\(\angle{ADC}=\frac{\pi}{4}\)である.
ここで, \(\frac{\pi}{4}=\angle{ADC}=\angle{ADB}+\angle{BDC}=2\angle{BCA}\)であるから, \(\angle{BCA}=\frac{\pi}{8}\)がわかる.
(2) 三角形\(ABC\)は\(AB=BC\)の二等辺三角形であり, (1)から\(\angle{BAC}=\angle{BCA}=\frac{\pi}{8}\)であるから,
$$
\angle{ABC}=\pi-\angle{BAC}-\angle{BCA}=\frac{3\pi}{4}
$$である. また, 三角形\(ACD\)は\(AC=CD\), \(AD=2\)となる直角二等辺三角形であるから, 三平方の定理から
$$
2^2={AD}^2={AC}^2+{CD}^2=2{AC}^2
$$
であるから, \(AC=\sqrt{2}\)である. よって, 三角形\(ABC\)で余弦定理から,
$$
\begin{align}
{AC}^2&={AB}^2+{BC}^2-2{AB}\cdot {BC}\cos{\angle{ABC}}\\[1.5ex]
\sqrt{2}^2&=2{BC}^2-2{BC}^2\cdot\left(-\frac{1}{\sqrt{2}}\right)\\[1.5ex]
{BC}^2&=\frac{2}{2+\sqrt{2}}\\[1.5ex]
{BC}&=\sqrt{\frac{2}{2+\sqrt{2}}}=\frac{\sqrt{2}}{\sqrt{2+\sqrt{2}}}=\frac{\sqrt{2}\sqrt{2-\sqrt{2}}}{\sqrt{2+\sqrt{2}}\sqrt{2-\sqrt{2}}}\\[1.5ex]
&=\frac{\sqrt{2}\sqrt{2-\sqrt{2}}}{\sqrt{2^2-\sqrt{2}^2}}=\frac{\sqrt{2}\sqrt{2-\sqrt{2}}}{\sqrt{2}}=\sqrt{2-\sqrt{2}}
\end{align}
$$
となり, \(BC\)が求まった.
(3) 三角形\(ADC\)において\(\angle{ADE}=\angle{CDE}\)より, \(DE\)は\(\angle{ADC}\)の二等分線である. また, \(AD=2\), \(CD=AC=\sqrt{2}\)であるから, 三角形の内角の二等分線の公式より, \(AE:EC=AD:CD=2:\sqrt{2}\)である. \(AE+EC=AC=\sqrt{2}\)に注意して,
$$
\triangle{BCE}=\triangle{ABC}\times\frac{EC}{AC}=\triangle{ABC}\times\frac{\sqrt{2}}{2+\sqrt{2}}
$$である.
ここで,
$$
\begin{align}
\triangle{ABC}&=\frac{1}{2}AB\cdot BC\sin{\angle{ABC}}=\frac{1}{2}\cdot\sqrt{2-\sqrt{2}}^2\times\frac{1}{\sqrt{2}}\\[1.5ex]
&=\frac{2-\sqrt{2}}{2\sqrt{2}}
\end{align}
$$
であるから,
$$
\begin{align}
\triangle{BCE}&=\frac{2-\sqrt{2}}{2\sqrt{2}}\times\frac{\sqrt{2}}{2+\sqrt{2}}=\frac{2-\sqrt{2}}{2(2+\sqrt{2})}\\[1.5ex]
&=\frac{(2-\sqrt{2})^2}{2(2+\sqrt{2})(2-\sqrt{2})}=\frac{2(\sqrt{2}-1)^2}{2^2}\\[1.5ex]
&=\frac{3-2\sqrt{2}}{2}
\end{align}
$$となる.
こういった図形問題は解答を見ると簡単に思えるのですが, 自分で導出するのはなかなか難しいです. 私は最初に解いたとき, (1)で余弦定理を用いて\(\cos{\angle{BCA}}\)を導出したのですが, その値が見たことのない値になったので, \(\cos\)の値から\(\angle{BCA}\)を求めることができませんでした. 最初に図をそれなりに綺麗に書けば, \(\angle{BCA}\)が\({30}^{\circ}\)より小さそうとはわかり, \({30}^{\circ}\)より小さい角の\(\cos\)は普通覚えていないということから, 余弦定理から求めることは難しそうであると気づくべきでした.
また, 今回の問題では三角形\(ADC\)において, \(AE\)が\(\angle{ADC}\)の二等分線になっていることに気づき, 二等分線の公式を使用できるかどうかがミソになっているかと思います. 受験の緊迫した状況の中で自分が思いつくか不安になりました.
youtubeでも解説しています.