【筑波大学入試】角の二等分線を扱うベクトルの問題(2024)

2025年7月12日

今回はこちらの問題を解いていきます.

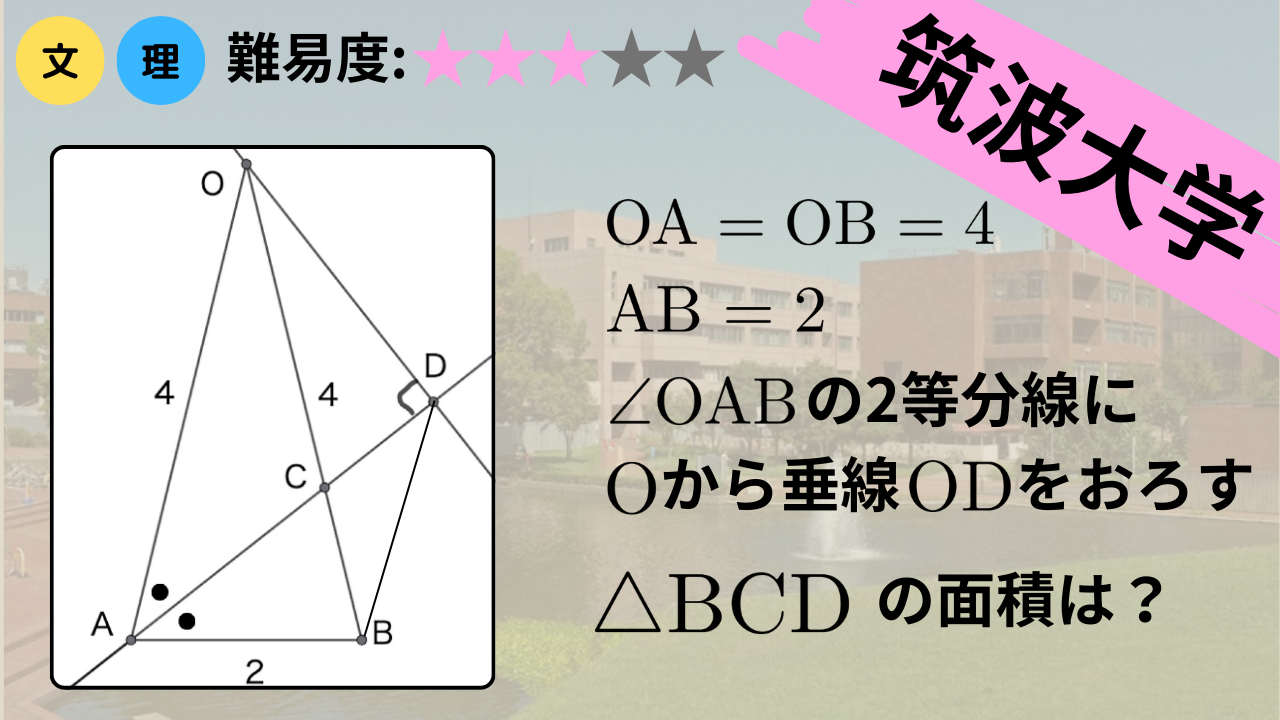
$\mathrm{OA}=\mathrm{OB}=4$, $\mathrm{AB}=2$である三角形$\triangle{\mathrm{OAB}}$がある. $\angle{\mathrm{OAB}}$の2等分線と線分$\mathrm{OB}$の交点を$C$とする. また$\mathrm{O}$から直線$\mathrm{AC}$に垂線をおろし, その足を$\mathrm{D}$とする. $\overrightarrow{\mathrm{OA}}=\overrightarrow{a}$, $\overrightarrow{\mathrm{OB}}=\overrightarrow{b}$として, 以下の問いに答えよ.

(1) $\overrightarrow{\mathrm{AC}}$, $\overrightarrow{\mathrm{OD}}$をそれぞれ$\overrightarrow{a}$, $\overrightarrow{b}$を用いて表せ.
(2) $\triangle{\mathrm{BCD}}$の面積を求めよ.
(2024 筑波大学理系[1])

こちら基本的な問題です. 角の二等分線の性質を使ったり, 線分の長さの比で面積を出したりするのですが, 図形問題が苦手でそのような方法を思いつかない向けに, ベクトルを使ったゴリゴリの別解も載せております.

先に問題文で与えられている条件をもとに図を描いておきます.

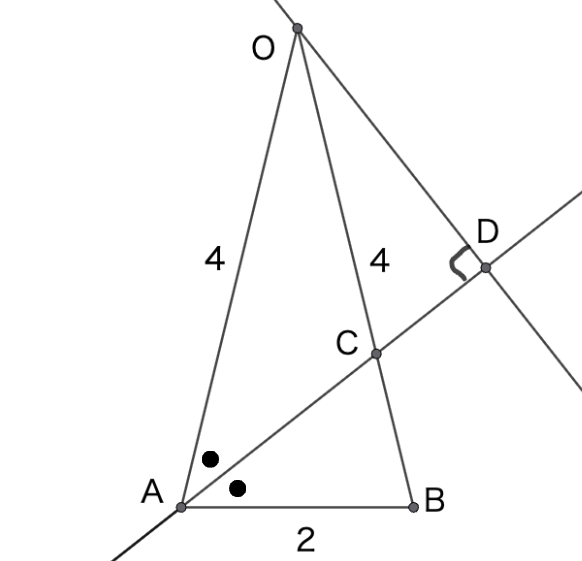
それでは解いていきましょう.

(1) $\triangle\mathrm{OAB}$で$\mathrm{AC}$は$\angle{\mathrm{OAB}}$の二等分線だから, 三角形の角の二等分線の性質から,
$$
\mathrm{BC}:\mathrm{OC}=\mathrm{AB}:\mathrm{OA}=2:4=1:2
$$となり, $\mathrm{C}$は線分$OB$を$2:1$に内分するから,
$$
\overrightarrow{\mathrm{OC}}=\frac{2}{3}\overrightarrow{\mathrm{OB}}=\frac{2}{3}\overrightarrow{b}
$$となる.よって,
$$
\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OA}}=\frac{2}{3}\overrightarrow{b}-\overrightarrow{a}
$$である.

また, $D$は直線$\mathrm{AC}$上にあるから, 実数$k$が存在して,
$$
\overrightarrow{\mathrm{AD}}=k \overrightarrow{\mathrm{AC}}
$$と表せるから,
$$
\begin{align}
\overrightarrow{\mathrm{OD}}&=\overrightarrow{\mathrm{OA}} +k \overrightarrow{\mathrm{AC}}=\overrightarrow{a}+k\left(\frac{2}{3}\overrightarrow{b}-\overrightarrow{a}\right)\\
&=(1-k)\overrightarrow{a}+\frac{2k}{3}\overrightarrow{b}
\end{align}
$$

$\overrightarrow{\mathrm{OD}}\perp \overrightarrow{\mathrm{AC}}$で, $\overrightarrow{\mathrm{OD}}\neq \overrightarrow{\mathrm{0}}$, $\overrightarrow{\mathrm{AC}}\neq \overrightarrow{\mathrm{0}}$だから, これは$\overrightarrow{\mathrm{OD}}\cdot \overrightarrow{\mathrm{AC}}=0$と同値である. この条件から$k$を求めるために, 先に$\overrightarrow{a}$と$\overrightarrow{b}$の内積$\overrightarrow{a}\cdot\overrightarrow{b}$を求める. 余弦定理から,
$$
\cos{\angle{\mathrm{AOB}}}=\frac{\mathrm{OA}^2+\mathrm{OB}^2-\mathrm{AB}^2}{2\mathrm{OA}\cdot \mathrm{OB} }=\frac{4^2+4^2-2^2}{2\cdot 4\cdot 4}=\frac{7}{8}
$$となり,
$$
\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos{\angle{\mathrm{AOB}}}=4\cdot 4 \cdot \frac{7}{8}=14
$$がわかる.

$\overrightarrow{\mathrm{OD}}\cdot \overrightarrow{\mathrm{AC}}=0$より,
$$
\begin{align}
\overrightarrow{\mathrm{OD}}\cdot \overrightarrow{\mathrm{AC}}=0&\iff \left((1-k)\overrightarrow{a}+\frac{2k}{3}\overrightarrow{b}\right)\cdot\left( \frac{2}{3}\overrightarrow{b}-\overrightarrow{a}\right)=0\\
&\iff \frac{2}{3}(1-k)\overrightarrow{a}\cdot \overrightarrow{b} -(1-k)|\overrightarrow{a}|^2+\frac{4}{9}k|\overrightarrow{b}|^2-\frac{2k}{3}\overrightarrow{a}\cdot \overrightarrow{b}=0\\
&\iff \frac{2}{3}\cdot 14(1-k) -4^2(1-k)+\frac{4\cdot 4^2}{9}k-\frac{2k\cdot 14}{3}=0\\
&(両辺に3^2=9をかけ分数の形を消し, 共通因数の4で割ると)\\
&\iff 21(1-k) -36(1-k)+16k-21k=0\\
&\iff 10k-15=0\\
&\iff k=\frac{3}{2}\\
\end{align}
$$
となり, $k$の値が求まる. よって,
$$
\overrightarrow{\mathrm{OD}}=\left(1-\frac{3}{2}\right)\overrightarrow{a}+\frac{2}{3}\cdot \frac{3}{2}\overrightarrow{b}=-\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}
$$がわかる.

(2) (1)より
$$
\overrightarrow{\mathrm{AD}}=\frac{3}{2}\overrightarrow{\mathrm{AC}}
$$であるから, $\triangle\mathrm{BAD}$で$\mathrm{BD}$を底辺と見たとき, $\mathrm{AC}:\mathrm{CD}=2:1$である. よって$\triangle{\mathrm{BAC}}$と$\triangle{\mathrm{BCD}}$の面積比も$2:1$となる. つまり,
$$
\triangle{\mathrm{BCD}}=\frac{1}{2}\triangle{\mathrm{BAC}}\,\,\, ・・・①
$$である.

また, $\mathrm{C}$は$\mathrm{AB}$を$2:1$に内分するから, $\mathrm{OB}:\mathrm{BC}=3:1$である. これから, $\triangle{\mathrm{OAB}}$に関して, $\mathrm{OB}$を底辺として見れば, $\triangle{\mathrm{OAB}}$と$\triangle{\mathrm{BAC}}$の面積比が$3:1$となることがわかる. つまり,
$$
\triangle{\mathrm{BAC}}=\frac{1}{3}\triangle{\mathrm{OAB}}\,\,\, ・・・②
$$である.

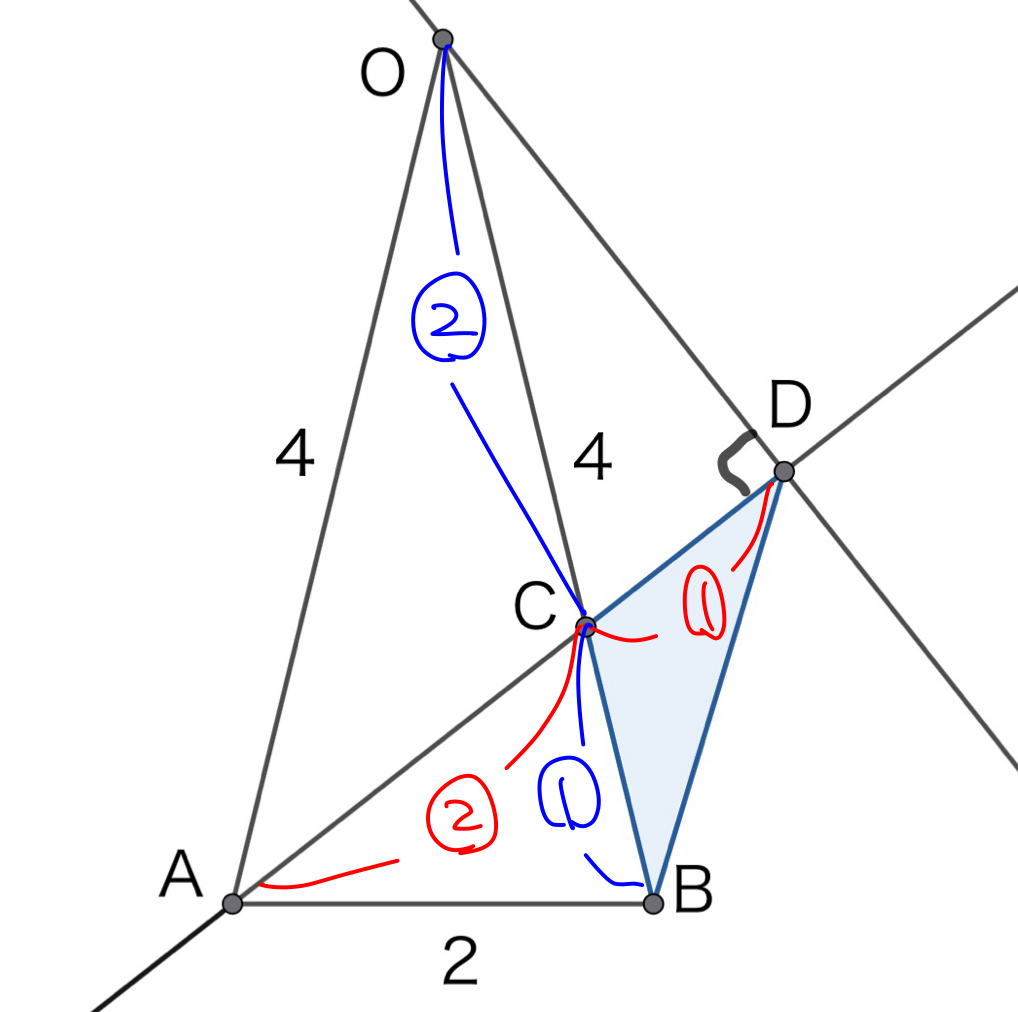
①, ②より,
$$
\triangle{\mathrm{BCD}}=\frac{1}{2}\triangle{\mathrm{BAC}}=\frac{1}{6}\triangle{\mathrm{OAB}}
$$となる.

よって, $\triangle{\mathrm{OAB}}$の面積を求めればよいが, これは2つのベクトルが作る三角形の面積の公式から,
$$
\triangle{\mathrm{OAB}}=\frac{1}{2}\sqrt{{\lvert \overrightarrow{a}\rvert}^2{\lvert \overrightarrow{b}\rvert}^2-\left(\overrightarrow{a}\cdot \overrightarrow{b}\right)^2}=\frac{1}{2}\sqrt{4^2\cdot 4^2 – 14^2}=\sqrt{15}
$$
となり, よって, $$
\triangle{\mathrm{BCD}}=\frac{\sqrt{15}}{6}
$$がわかる.

とても基本的な問題ですが, いくつか注意事項と別解を記載します.

まず, $\overrightarrow{a}\cdot \overrightarrow{b}$を計算するために, 余弦定理を使いましたが, $\mathrm{AB}=\left|\overrightarrow{b}-\overrightarrow{a}\right|(=2) $が求まっているので, 以下のように求めることもできます.

$$
\begin{align}
\mathrm{AB}^2= 2^2&=\left|\overrightarrow{b}-\overrightarrow{a}\right|^2=(\overrightarrow{b}-\overrightarrow{a})\cdot(\overrightarrow{b}-\overrightarrow{a})\\
&=|\overrightarrow{a}|^2-2\overrightarrow{a}\cdot \overrightarrow{b}+|\overrightarrow{b}|^2\\
&=16-2\overrightarrow{a}\cdot \overrightarrow{b}+16\\
\iff & \overrightarrow{a}\cdot \overrightarrow{b}=14
\end{align}
$$

また, $\overrightarrow{a}$と$\overrightarrow{b}$が作る三角形の面積が$\frac{1}{2}\sqrt{{\lvert \overrightarrow{a}\rvert}^2{\lvert \overrightarrow{b}\rvert}^2-\left(\overrightarrow{a}\cdot \overrightarrow{b}\right)^2}$となる公式の証明を以下で与えておきます.

$\overrightarrow{a}$と$\overrightarrow{b}$のなす角を$\theta$とする.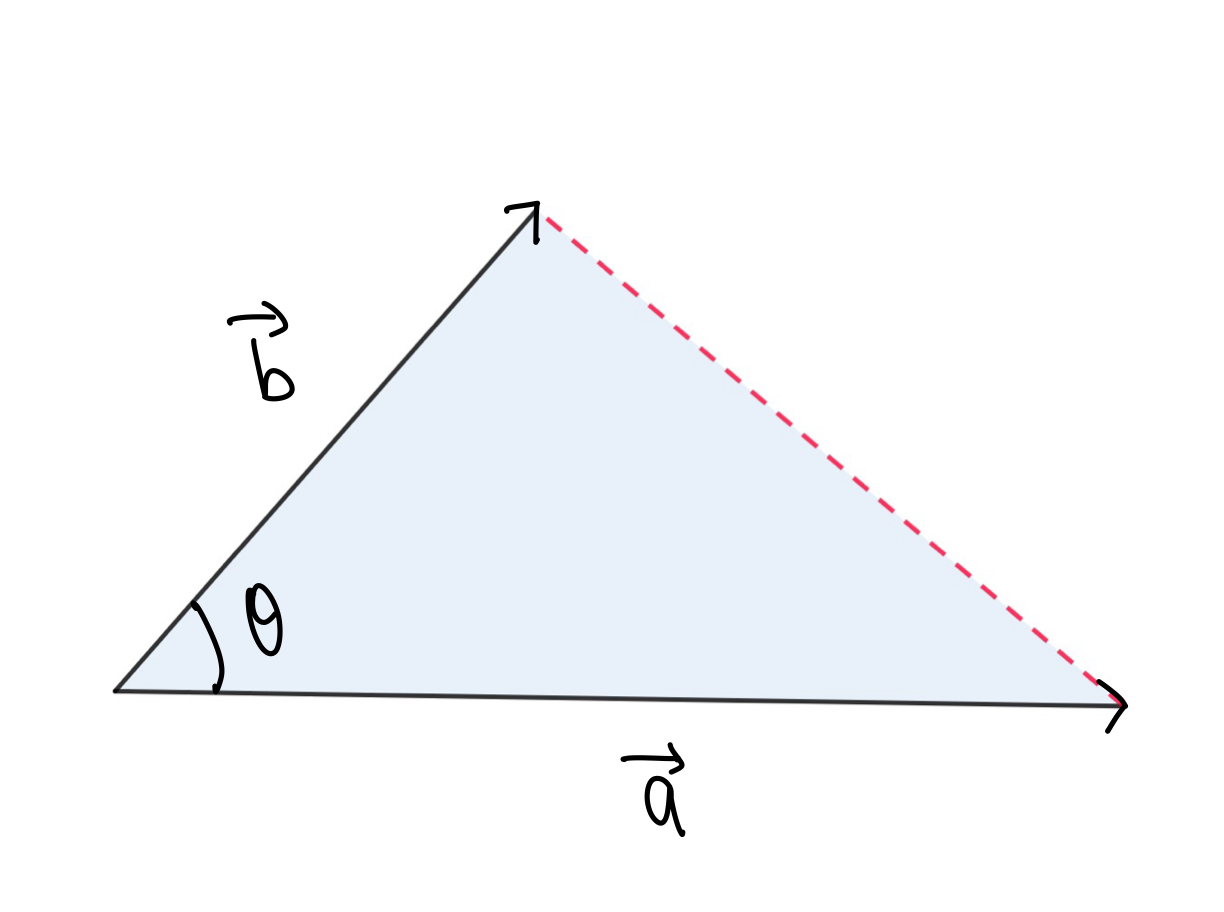

内積の定義から,
$$
\cos{\theta}=\frac{\overrightarrow{a}\cdot \overrightarrow{b} }{|\overrightarrow{a}||\overrightarrow{b}|}
$$となる. これから,
$$
\sin{\theta}=\sqrt{1-\cos^2{\theta}}=\sqrt{1-\left(\frac{\overrightarrow{a}\cdot \overrightarrow{b} }{|\overrightarrow{a}||\overrightarrow{b}|}\right)^2}
$$となる.
2辺の長さが$a$, $b$, その間の角が$\theta$のとき, その三角形の面積は, $\frac{1}{2}ab\sin{\theta}$と表せるから, $\overrightarrow{a}$と$\overrightarrow{b}$が作る三角形の面積は,
$$
\begin{align}
\frac{1}{2}|\overrightarrow{a}||\overrightarrow{b}|\sin{\theta}&=\frac{1}{2}|\overrightarrow{a}||\overrightarrow{b}|\sqrt{1-\left(\frac{\overrightarrow{a}\cdot \overrightarrow{b} }{|\overrightarrow{a}||\overrightarrow{b}|}\right)^2}\\
&=\frac{1}{2}\sqrt{{\lvert \overrightarrow{a}\rvert}^2{\lvert \overrightarrow{b}\rvert}^2-\left(\overrightarrow{a}\cdot \overrightarrow{b}\right)^2}
\end{align}
$$
となる.

最後に, 先の解答中の2箇所の議論に関してそれぞれ別解を紹介します.

まず1つ目は$\overrightarrow{\mathrm{OC}}$を求める箇所です. 先の解答では, 角の二等分線の性質から$\mathrm{BC}:\mathrm{OC}=1:2$を導出し$\overrightarrow{\mathrm{OC}}$を求めました. ここでは, 角の二等分線の性質を使うことを思いつかない方向けに$\overrightarrow{\mathrm{OC}}$を求める別解を紹介します.

以下の図も参考に, 一般に$\overrightarrow{a}$と$\overrightarrow{b}$のなす角の2等分線の方向を向くベクトルは,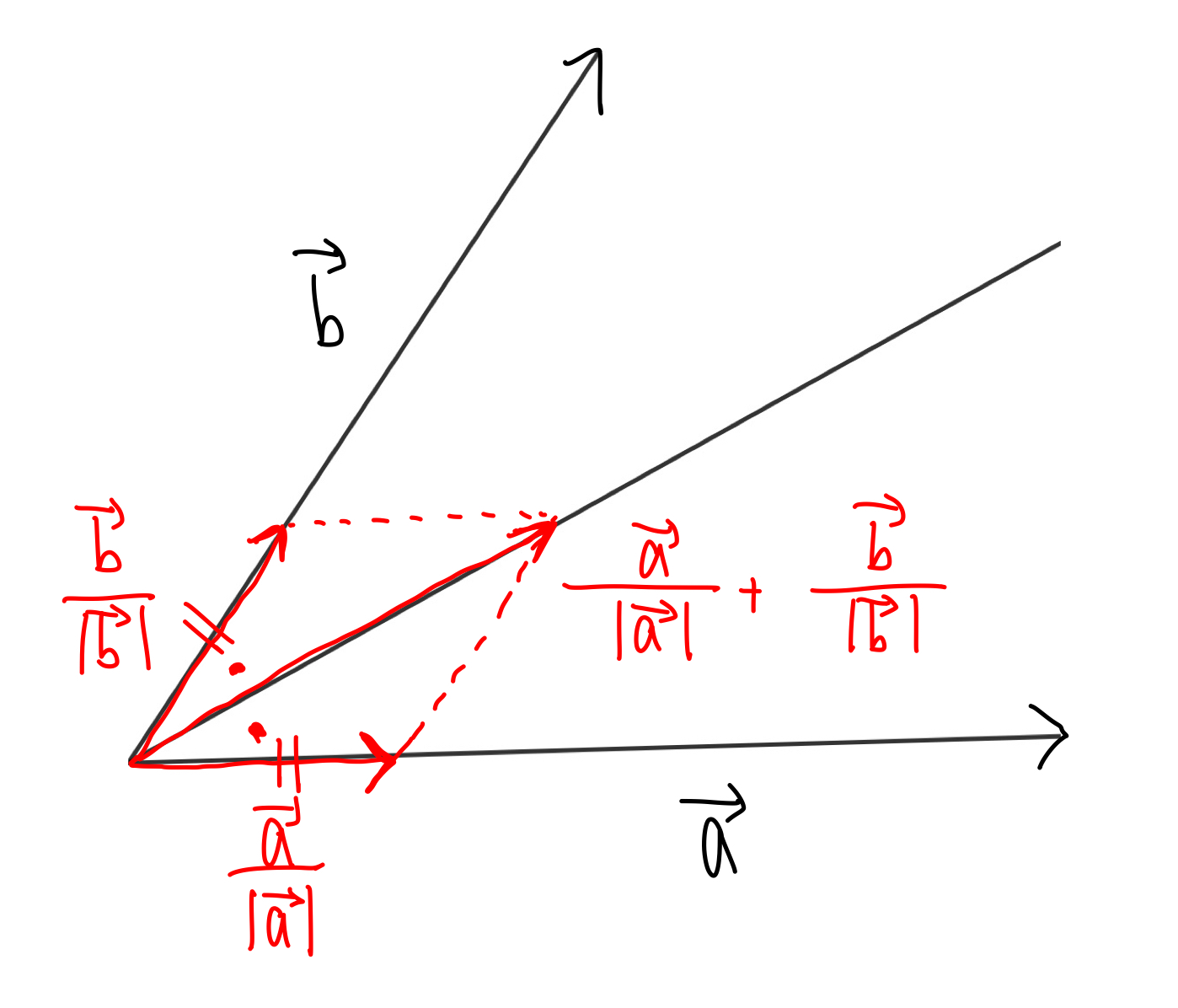

$$
\frac{\overrightarrow{a} }{|\overrightarrow{a}|}+\frac{\overrightarrow{b} }{|\overrightarrow{b}|}
$$となるから, 実数$t$を用いて,
$$
\begin{align}
\overrightarrow{\mathrm{AC}}
&= t\left( \frac{ \overrightarrow{\mathrm{OA}} }{ \left| \overrightarrow{\mathrm{OA}} \right| } + \frac{ \overrightarrow{\mathrm{AB}} }{ \left| \overrightarrow{\mathrm{AB}} \right| } \right) \\
&= t\left( -\frac{ \overrightarrow{a} }{4} + \frac{ \overrightarrow{b} – \overrightarrow{a} }{2} \right) \\
&= t\left( -\frac{3}{4} \overrightarrow{a} + \frac{1}{2} \overrightarrow{b} \right)
\end{align}
$$と表せる.
よって, $\overrightarrow{\mathrm{OC}}$は,
$$
\begin{align}
\overrightarrow{\mathrm{OC}}
&= \overrightarrow{\mathrm{OA}} + \overrightarrow{\mathrm{AC}} \\
&= \overrightarrow{a} + t\left( -\frac{3}{4} \overrightarrow{a} + \frac{1}{2} \overrightarrow{b} \right) \\
&= \left(1 – \frac{3}{4}t\right)\overrightarrow{a} + \frac{1}{2}t \overrightarrow{b}
\end{align}
$$
と書ける. ここで, $\mathrm{C}$は辺$\mathrm{OB}$上にあるので, 実数$s$が存在して,
$$
\overrightarrow{\mathrm{OC}}=s \overrightarrow{b}
$$
の形で表せ, $\overrightarrow{\mathrm{OC}}$の$\overrightarrow{a}$, $\overrightarrow{b}$での表し方は一通りなので,
$$t-\frac{3}{4}=0, \,\,\frac{1}{2}t=s
$$となり, これから$t=\frac{4}{3}$, $s=\frac{2}{3}$であることがわかる. よって,
$$
\overrightarrow{\mathrm{OC}}=\frac{2}{3}\overrightarrow{b}
$$となる.

次の別解は$\triangle{\mathrm{BCD}}$の面積を求める箇所です. 先の回答では高さが等しい2つの三角形の面積比が底辺の長さの比になることを用いて求めましたが, このような解法を思いつかない向けに, ゴリゴリと計算を行う方法です.

$\triangle{\mathrm{BCD}}$は$\overrightarrow{\mathrm{CB}}$, $\overrightarrow{\mathrm{BD}}$がなす三角形であり,
$$
\begin{align}
\overrightarrow{\mathrm{CB}}&=\frac{1}{3}\overrightarrow{b}\\
\overrightarrow{\mathrm{CD}}&=\overrightarrow{\mathrm{OD}}-\overrightarrow{\mathrm{OC}}=\left(-\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}\right)-\frac{2}{3}\overrightarrow{b}\\
&=-\frac{1}{2}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}
\end{align}
$$
であるから, $\triangle{\mathrm{BCD}}$の面積は,
$$
\triangle{\mathrm{BCD}}=\frac{1}{2}\sqrt{\left| \overrightarrow{\mathrm{CB} }\right|^2\left| \overrightarrow{\mathrm{CD} }\right|^2-\left(\overrightarrow{\mathrm{CB}}\cdot \overrightarrow{\mathrm{CD}}\right)^2}$$
である.
ここで,
$$
\begin{align}
\left|\overrightarrow{\mathrm{CB}}\right|&=\frac{4}{3}\\
\left|\overrightarrow{\mathrm{CD}}\right|&=\left|-\frac{1}{2}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}\right|=\sqrt{\left(-\frac{1}{2}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}\right)\cdot\left(-\frac{1}{2}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}\right)}\\
&=\sqrt{\frac{1}{4}\left|\overrightarrow{a} \right|^2-\frac{1}{3}\overrightarrow{a}\cdot \overrightarrow{b}+\frac{1}{9}\left|\overrightarrow{b}\right|^2 }
=\sqrt{\frac{1}{4}\cdot 4^2-\frac{1}{3}\cdot 14+\frac{1}{9}\cdot 4^2 }\\
&=\sqrt{4-\frac{14}{3}+\frac{16}{9}}=\frac{\sqrt{10}}{3}\\
\overrightarrow{\mathrm{CB}}\cdot \overrightarrow{\mathrm{CD}}&=\frac{1}{3}\overrightarrow{b}\cdot\left(-\frac{1}{2}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}\right)\\
&=-\frac{1}{6}\overrightarrow{a}\cdot \overrightarrow{b}+\frac{1}{9}\left|\overrightarrow{b}\right|^2\\
&=-\frac{1}{6}\cdot 14+\frac{16}{9}=-\frac{5}{9}
\end{align}
$$となり, 最終的に$\triangle{\mathrm{BCD}}$の面積は,
$$
\begin{align}
\triangle{\mathrm{BCD}}&=\frac{1}{2}\sqrt{\left(\frac{4}{3}\right)^2\left(\frac{\sqrt{10}}{3}\right)^2-\left(-\frac{5}{9}\right)^2}\\
&=\frac{1}{2}\sqrt{\frac{160}{9^2}-\frac{25}{9^2}}=\frac{1}{2}\sqrt{\frac{135}{9^2}}=\frac{\sqrt{15}}{6}
\end{align}
$$となる.