【東京大学入試】∠APC=∠BPCを満たす点Pの軌跡を求めよ！(2008)

\(\mathrm{P}\)の座標を\((X,Y)\)とおく. \(\angle{\mathrm{APC}}\), \(\angle{\mathrm{BPC}}\)は共に\(0^\circ\)以上\(180^\circ\)以下なので,$$
\angle{\mathrm{APC}}=\angle{\mathrm{BPC}}\iff \cos{\angle{\mathrm{APC}}}=\cos{\angle{\mathrm{BPC}}}
$$である.
\(\triangle{\mathrm{APC}}\)と\(\triangle{\mathrm{BPC}}\)で余弦定理から,$$
\begin{align}
\cos{\angle{\mathrm{APC}}}&=\frac{\mathrm{AP}^2+\mathrm{CP}^2-\mathrm{AC}^2}{2\mathrm{AP}\cdot \mathrm{CP}}\\[1.5ex]
\cos{\angle{\mathrm{BPC}}}&=\frac{\mathrm{BP}^2+\mathrm{BP}^2-\mathrm{BC}^2}{2\mathrm{BP}\cdot \mathrm{CP}}\\[1.5ex]
\end{align}
$$であるから,$$
\begin{align}
&\cos{\angle{\mathrm{APC}}}=\cos{\angle{\mathrm{BPC}}}\\[1.5ex]
\iff & \frac{\mathrm{AP}^2+\mathrm{CP}^2-\mathrm{AC}^2}{2\mathrm{AP}\cdot \mathrm{CP}} = \frac{\mathrm{BP}^2+\mathrm{BP}^2-\mathrm{BC}^2}{2\mathrm{BP}\cdot \mathrm{CP}}\\[1.5ex]
\iff & \frac{\mathrm{AP}^2+\mathrm{CP}^2-\mathrm{AC}^2}{\mathrm{AP}} = \frac{\mathrm{BP}^2+\mathrm{BP}^2-\mathrm{BC}^2}{\mathrm{BP}}\\[1.5ex]
\iff & \frac{(X-1)^2+Y^2+X^2+(Y+1)^2-2}{\sqrt{(X-1)^2+Y^2}} =\frac{(X+1)^2+Y^2+X^2+(Y+1)^2-2}{\sqrt{(X+1)^2+Y^2}} \\[1.5ex]
\iff & \frac{X^2+Y^2-X+Y}{\sqrt{(X-1)^2+Y^2}} =\frac{X^2+Y^2+X+Y}{\sqrt{(X+1)^2+Y^2}} \\[1.5ex]
\end{align}
$$となる. 一般に,$$
a=b\iff a^2+b^2,\,\,かつ\,\,ab\geq 0
$$であるから, これは,$$
\begin{align}
&\frac{(X^2+Y^2-X+Y)^2}{(X-1)^2+Y^2} =\frac{(X^2+Y^2+X+Y)^2}{(X+1)^2+Y^2}\\[1.5ex]
かつ \,\,\,\,&(X^2+Y^2-X+Y)(X^2+Y^2+X+Y)\geq 0
\end{align}
$$と同値である.

1番目の条件式は\(Z=X^2+Y^2\)とおいて,$$
(Z+Y-X)^2(Z+1+2X)=(Z+Y+X)^2(Z+1-2X)
$$となる. この両辺は\(X\)の符号が異なるだけなので, 各辺を展開しての\(X\)の\(3\)次式として見たときに, 定数項と\(X\)の\(2\)次の項は両辺で打ち消し合い, \(X\)の\(1\)次, \(3\)次だけ残ることがわかる. これから,$$
\begin{align}
&X(Z+Y)^2-X(Z+Y)(Z+1)+X^3\\[1.5ex]
\iff & X(Z^2+2YZ+Y^2-Z^2-Z-YZ-Y+X^2)=0\\[1.5ex]
\iff & XY(Z-1)=0\\[1.5ex]
\iff & XY(X^2+Y^2-1)=0\\[1.5ex]
\iff & X=0\,\,または\,\,Y=0\,\,または\,\,X^2+Y^2=1
\end{align}
$$と表すことができる.

次に, 2番目の条件式は,$$
\begin{align}
&(X^2+Y^2-X+Y)(X^2+Y^2+X+Y)\geq 0\\[1.5ex]
\iff & \left\{\left(X-\frac{1}{2}\right)^2+\left(Y+\frac{1}{2}\right)^2-\frac{1}{2}\right\}\left\{\left(X+\frac{1}{2}\right)^2+\left(Y+\frac{1}{2}\right)^2-\frac{1}{2}\right\}\geq 0\\[1.5ex]
\iff & 「\left(X-\frac{1}{2}\right)^2+\left(Y+\frac{1}{2}\right)^2-\frac{1}{2} \geq 0\,\,かつ\,\,\left(X+\frac{1}{2}\right)^2+\left(Y+\frac{1}{2}\right)^2-\frac{1}{2}\geq 0」\\[1.5ex]
& または\\[1.5ex]
&「\left(X-\frac{1}{2}\right)^2+\left(Y+\frac{1}{2}\right)^2-\frac{1}{2} \leq 0\,\,かつ\,\,\left(X+\frac{1}{2}\right)^2+\left(Y+\frac{1}{2}\right)^2-\frac{1}{2}\leq 0」
\end{align}
$$となる.

よって, 2つの条件を共に満たす領域(問題文の前提から\(\mathrm{A}\), \(\mathrm{B}\), \(\mathrm{C}\)を除いている)$$
\begin{align}
&「x^2+y^2=1\,\,かつ\,\,y>0 」\\[1.5ex]
& または\\[1.5ex]
&「x=0\,\,かつ\,\,y\neq -1 」\\[1.5ex]
& または\\[1.5ex]
&「y=0\,\,かつ\,\, |x|>1」\\[1.5ex]
\end{align}
$$となり, \(\mathrm{P}\)の軌跡を図示すると

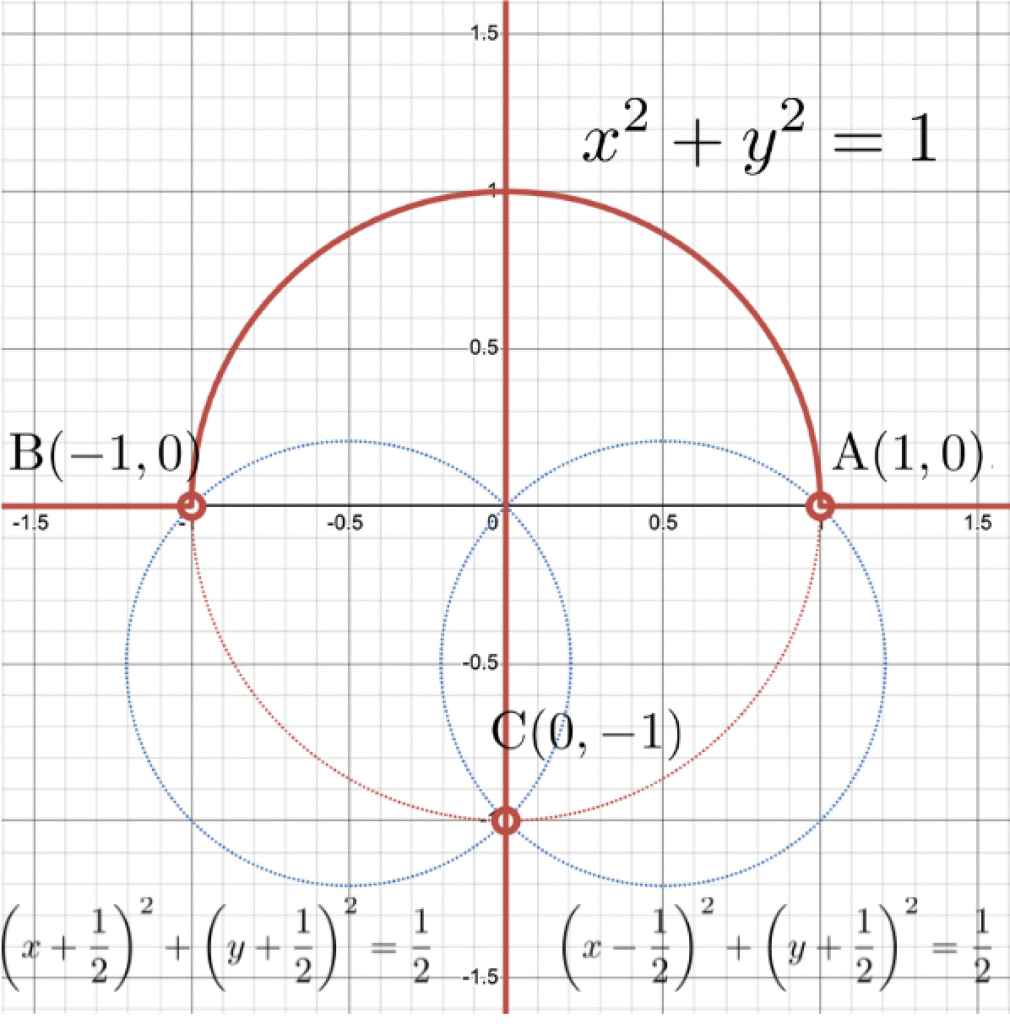
となる.