今回はこちらの問題を解いていきます.
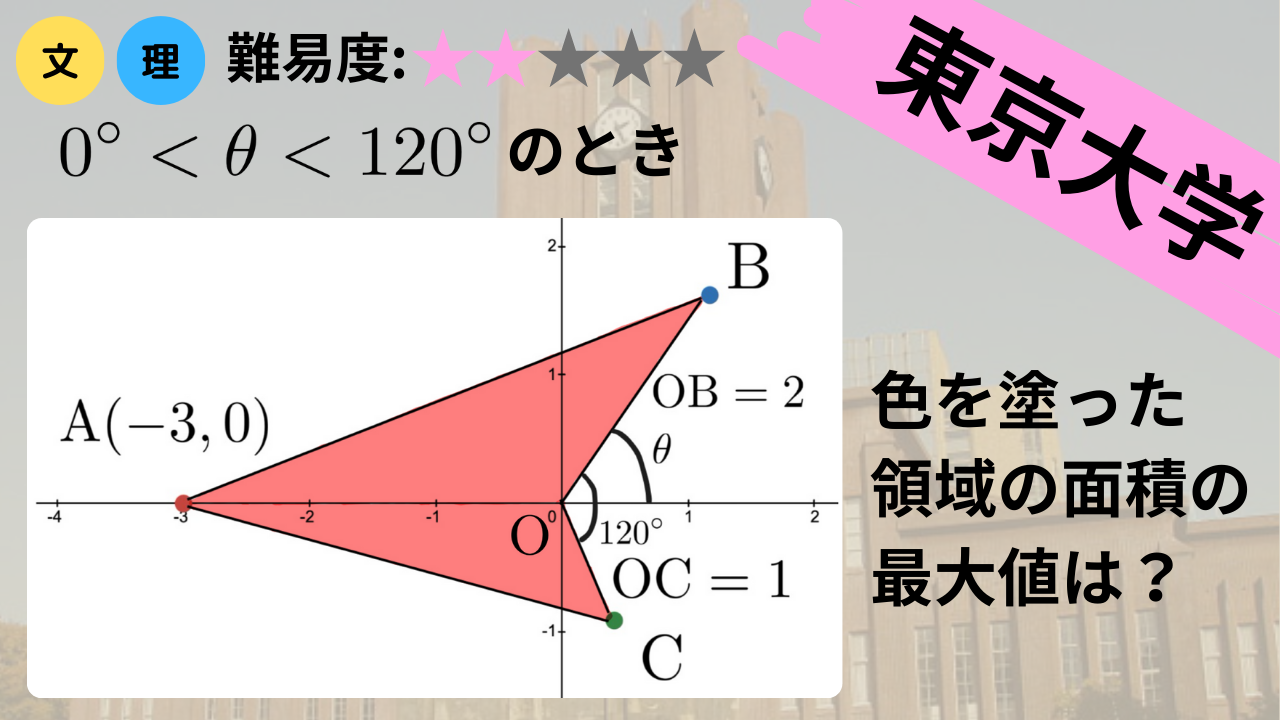
\(\mathrm{O}\)を原点とする座標平面上に点\(\mathrm{A}(-3,0)\)をとり, \(0^\circ < \theta < 120^\circ\)の範囲にある\(\theta\)に対して, 次の条件\((\mathrm{i})\), \((\mathrm{ii})\)をみたす\(2\)点\(\mathrm{B}\), \(\mathrm{C}\)を考える.
\((\mathrm{i})\) \(\mathrm{B}\)は\(y>0\)の部分にあり, \(\mathrm{OB}=2\)かつ\(\angle{\mathrm{AOB}}=180^\circ-\theta\)である.
\((\mathrm{ii})\) \(\mathrm{C}\)は\(y<0\)の部分にあり, \(\mathrm{OC}=1\)かつ\(\angle{\mathrm{BOC}}=120^\circ\)である. ただし, \(\triangle\mathrm{ABC}\)は\(\mathrm{O}\)を含むものとする.
このとき, 以下の問いに答えよ.
(1) \(\triangle\mathrm{OAB}\)と\(\triangle\mathrm{OAC}\)の面積が等しいとき, \(\theta\)の値を求めよ.
(2) \(\theta\)を\(0^\circ < \theta < 120^\circ\)の範囲で動かすとき, \(\triangle\mathrm{OAB}\)と\(\triangle\mathrm{OAC}\)の面積の和が最大値と, そのときの\(\sin{\theta}\)の値を求めよ.
(2010 東京大学 文系 [1])
それでは解いていきましょう.
(1) \(\mathrm{B}\), \(\mathrm{C}\)を図示すると以下のようになり, 座標はそれぞれ, \((2\cos{\theta}, 2\sin{\theta})\), \((\cos{(\theta-120^\circ)}, \sin{(\theta-120^\circ)})\)となる.
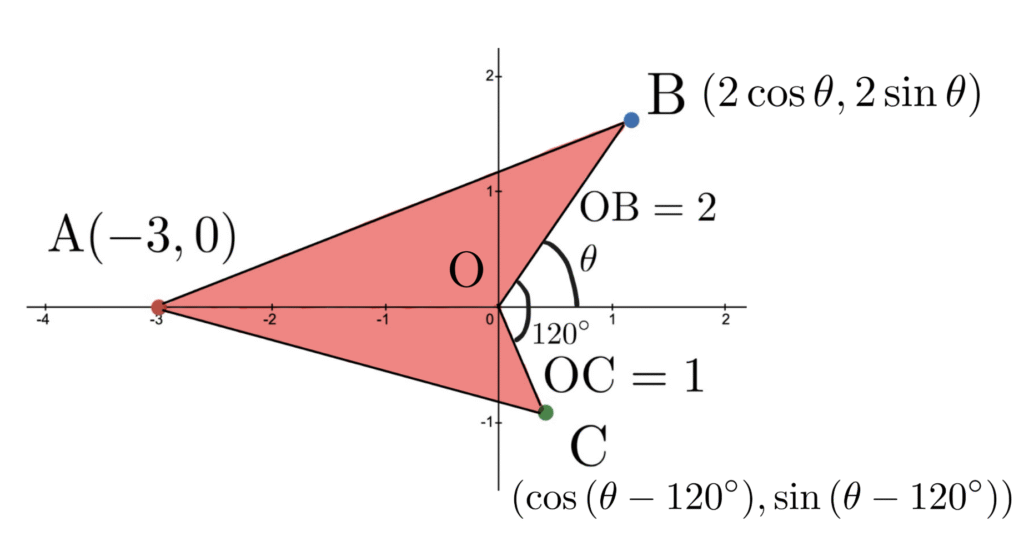
\(\triangle\mathrm{OAB}\)と\(\triangle\mathrm{OAC}\)は辺\(\mathrm{OA}\)を共有し, その面積が等しくなるのは, 辺\(\mathrm{OA}\)を底辺として見たときの高さ\(\mathrm{B}\), \(\mathrm{C}\)の\(y\)座標の絶対値が等しいときである. \(\mathrm{B}\)の\(y\)座標は常に正, \(\mathrm{C}\)の\(y\)座標は常に負なので, この条件は,$$
2\sin{\theta}=-\sin{(\theta-120^\circ)}
$$である. これを変形すると,$$
\begin{align}
2\sin{\theta}&=\frac{1}{2}\sin{\theta}+\frac{\sqrt{3}}{2}\cos{\theta}\\[1.5ex]
\frac{3}{2}\sin{\theta}&=\frac{\sqrt{3}}{2}\cos{\theta}\\[1.5ex]
\sqrt{3}\sin{\theta}&=\cos{\theta}
\end{align}
$$である. \(\theta=90^\circ\)はこの方程式の解ではないので, \(\theta\neq 90^\circ\)である. このとき, \(\cos{\theta}\neq 0\)であるから, 両辺を\(\sqrt{3}\cos{\theta}\)で割って,$$
\tan{\theta}=\frac{1}{\sqrt{3}}
$$となり, \(0^\circ < \theta < 120^\circ\)より, \(\theta=30^\circ\)である.
(2) \(\triangle\mathrm{OAB}\)と\(\triangle\mathrm{OAC}\)の面積の和\(S\)は,$$
S=\frac{1}{2}\times 3\times2\sin{\theta}+\frac{1}{2}\times 3\times \left\{-\sin{(\theta-120^\circ)}\right\}
$$であり, これから, $$
\begin{align}
S&=3\sin{\theta}+\frac{3}{2}\left(\frac{1}{2}\sin{\theta}+\frac{\sqrt{3}}{2}\cos{\theta}\right)\\[1.5ex]
&=\frac{15}{4}\sin{\theta}+\frac{3\sqrt{3}}{4}\cos{\theta}\\[1.5ex]
&=\frac{3}{4}\left(5\sin{\theta}+\sqrt{3}\cos{\theta}\right)\\[1.5ex]&=\frac{3}{4}\sqrt{5^2+3}\left(\sin{\theta}\cdot \frac{5}{2\sqrt{7}}+\cos{\theta}\cdot\frac{\sqrt{3}}{2\sqrt{7}}\right)\\[1.5ex]
&=\frac{3\sqrt{7}}{2}\left(\sin{\theta}\cos{\alpha}+\cos{\theta}\sin{\alpha}\right)\\[1.5ex]
&=\frac{3\sqrt{7}}{2}\sin{(\theta+\alpha)}
\end{align}
$$でとなる. ここで, \(\alpha\)は\(\displaystyle \cos{\alpha}=\frac{5}{2\sqrt{7}}\), \(\displaystyle \sin{\alpha}=\frac{\sqrt{3}}{2\sqrt{7}}\)を満たす角度である.
\(\cos{\alpha}>0\), \(\sin{\alpha}>0\)より, \(0^\circ <\alpha < 90^\circ\)がわかり, これから,$$
0^\circ<\alpha<\theta+\alpha<\alpha+120^\circ<210^\circ
$$となる. \(0^\circ<\theta+\alpha<210^\circ\)の範囲では, \(S\)は\(\theta+\alpha=90^\circ\)のときに, 最大となる. \(0^\circ<\theta(=90^\circ -\alpha)<90^\circ\)より, これを満たす\(\theta\)はたしかに\(0^\circ < \theta < 120^\circ\)の範囲に存在することがわかる.
\(S\)の最大値は\( \displaystyle \frac{3\sqrt{7}}{2}\)であり, このとき, \(\sin{\theta}\)は,$$
\sin{\theta}=\sin{(90^\circ – \alpha)}=\cos{\alpha}=\frac{5}{2\sqrt{7}}=\frac{5\sqrt{7}}{14}
$$となる.
youtubeでも解説しています.