【東京大学入試】2つの円に内接・外接する円の中心と最大の高さ(2009)

円\(C_1\), \(C_2\), \(C_3\)の中心をそれぞれ\(\mathrm{O}(0,0)\), \(\mathrm{O_2}(1,0)\), \(\mathrm{O_3}(a,b)\)とおくと, \(C_3\)と\(C_1\)に内接することから,$$
\begin{align}
&\mathrm{OO_3}+t=2\\[1.5ex]
\iff & \sqrt{a^2+b^2}=2-t
\end{align}
$$であり, \(C_2\)と\(C_3\)が外接することから,$$
\begin{align}
&\mathrm{O_2O_3}=1+t\\[1.5ex]
\iff & \sqrt{(a-1)^2+b^2}=1+t
\end{align}
$$である.

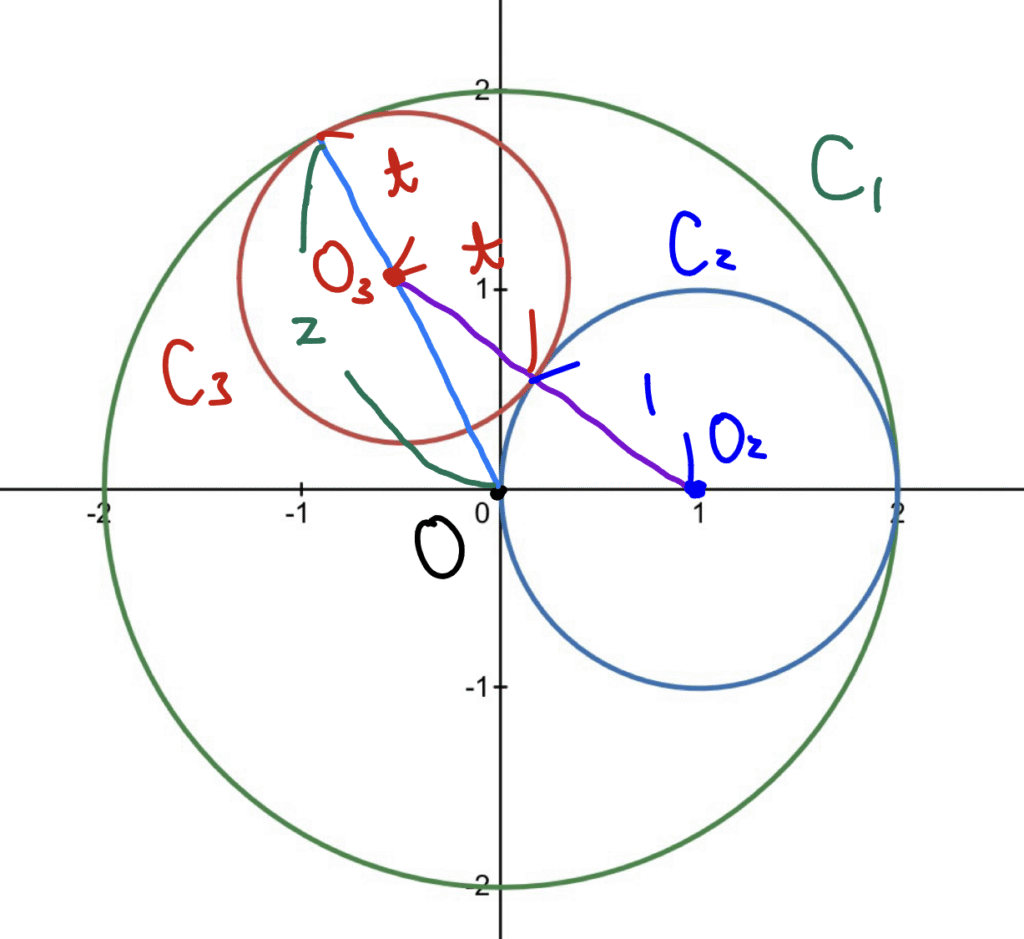
\(b\)は正の実数であるから, \(2-t=\sqrt{a^2+b^2}>0\), \(1+t=\sqrt{(a-1)^2+b^2}>0\)であるから, 「\(2-t>0\)かつ, \(1+t>0\)」つまり, 「\(-1<t<2\)」である必要があり, この範囲では\(2\)式で両辺を平方しても同値関係は崩れない.$$
\begin{align}
& \sqrt{a^2+b^2}=2-t\\[1.5ex]
\iff & a^2+b^2=(2-t)^2\\[1.5ex]
& \sqrt{(a-1)^2+b^2}=1+t\\[1.5ex]
\iff & (a-1)^2+b^2=(1+t)^2\\[1.5ex]
\end{align}
$$平方した\(2\)式で辺々を引くと,$$
\begin{align}
& a^2-(a-1)^2=(2-t)^2-(1+t)^2\\[1.5ex]
\iff & 2a-1=-6t+3\\[1.5ex]
\iff & a=-3t+2
\end{align}
$$であり, これを\(a^2+b^2=(2-t)^2\)に代入して,$$
\begin{align}
&(-3t+2)^2+b^2=(2-t)^2\\[1.5ex]
\iff & b^2=8t-8t^2
\end{align}
$$となる. ここで, \(b\)は正の実数より, \(b^2>0\)であるから, \(t\)は$$
\begin{align}
& b^2=8t-8t^2>0\\[1.5ex]
\iff & t(t-1)<0\\[1.5ex]
\iff & 0<t<1
\end{align}
$$となる必要がある. そしてこのとき, \(b\)は正より$$
b=\sqrt{8t-8t^2}
$$がわかる. よって,$$
\begin{align}
a&=-3t+2\\[1.5ex]
b&=\sqrt{8t-8t^2}
\end{align}
$$である. また, \(t\)がとり得る値の範囲は, 先に求めた2つの必要条件「\(-1<t<2\)」,「\(0<t<2\)」と, \(t\)は円\(C_3\)の半径であるから「\(t>0\)」の共通範囲として, \(0<t<1\)となる必要があり, 逆にこの範囲で条件を満たす\(a\), \(b\)が求まったのでこれは十分条件でもある. よって\(t\)のとり得る値の範囲は,$$
0<t<1
$$である.

(2) \(b\)は正の実数であるから, \(b^2\)が最大のとき, \(b\)もまた最大になる. $$
b^2=8t-8t^2=-8\left(t-\frac{1}{2}\right)^2+2
$$であり, \(0<t<1\)より\(b^2\)は\(\displaystyle t=\frac{1}{2}\)のとき最大値\(2\)をとることがわかる.

よって\(b\)は\(\displaystyle t=\frac{1}{2}\)のとき最大値\(\sqrt{2}\)をとる.