今回はこちらの問題を解いていきます.
\(2\)次以下の整式\(f(x)=ax^2+bx+c\)に対し,$$
S=\int_0^2\left|f^\prime(x)\right|\,dx
$$を考える.
(1) \(f(0)=0\), \(f(2)=2\)のとき, \(S\)を\(a\)の関数として表せ.
(2) \(f(0)=0\), \(f(2)=2\)を満たしながら\(f\)が変化するとき, \(S\)の最小値を求めよ.
(2009 東京大学 文系 [4])
それでは解いていきましょう.
(1) \(f(0)=0\), \(f(2)=2\)より,$$
\begin{align}
f(0)&=c=0\\[1.5ex]
f(2)&=4a+2b+c=2\\[1.5ex]
\end{align}
$$となり, \(c=0\), \(b=1-2a\)がわかる. よって\(f(x)=ax^2+(1-2a)x\)となり,$$
f^\prime(x)=2ax+1-2a
$$である.
① \( \displaystyle a\leq-\frac{1}{2}\)のとき
\(y=|f^(x)|\)のグラフは以下のようになり,
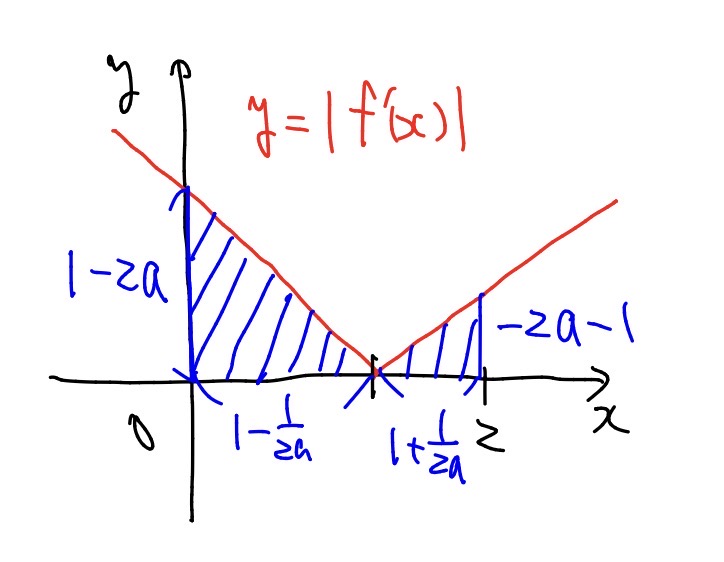
\(S\)は斜線部の面積なので,$$
\begin{align}
S&=\frac{1}{2}\left(1-\frac{1}{2a}\right)(1-2a)+\frac{1}{2}\left(1+\frac{1}{2a}\right)(2a-1)\\[1.5ex]
&=\frac{1}{2}\left(1-2a-\frac{1}{2a}+1-2a-1-1-\frac{1}{2a}\right)\\[1.5ex]
&=-2a-\frac{1}{2a}
\end{align}
$$となる.
② \(\displaystyle -\frac{1}{2}< a < \frac{1}{2}\)のとき
\(y=|f^\prime(x)|\)のグラフは以下のようになり,
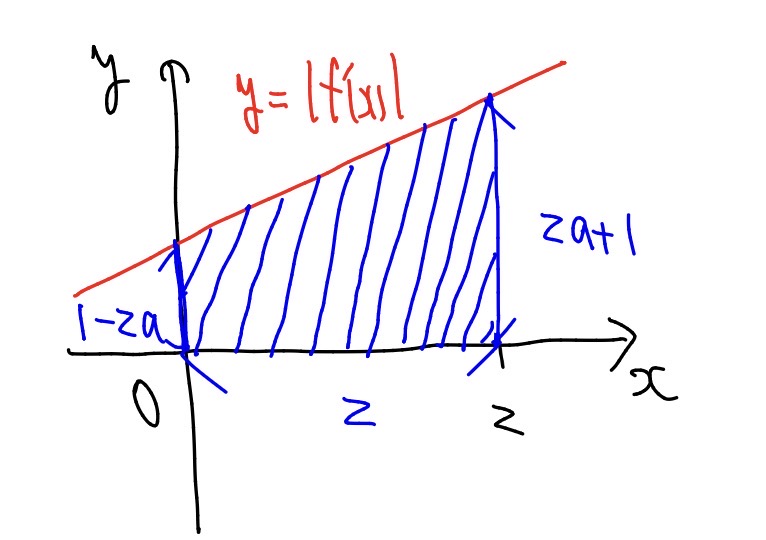
\(S\)は斜線部の面積なので,$$
S=\left\{(1-2a)+(2a+1)\right\}\times 2 \times \frac{1}{2}=2
$$となる.
③ \(\displaystyle a\geq\frac{1}{2}\)のとき
\(y=|f^\prime(x)|\)のグラフは以下のようになり,
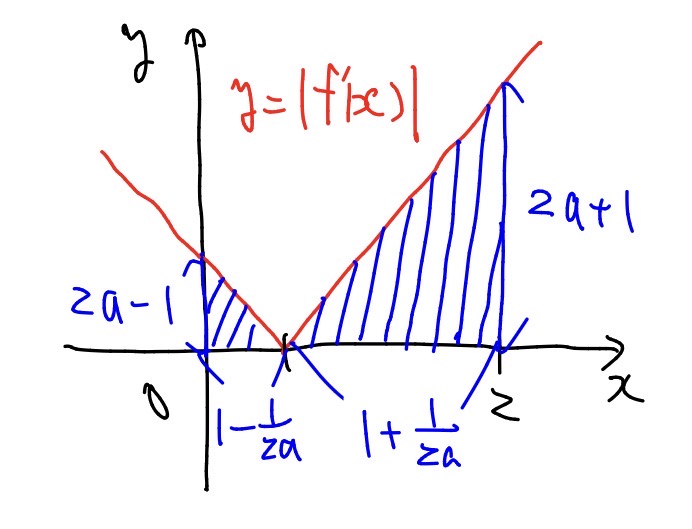
\(S\)は斜線部の面積なので,$$
\begin{align}
S&=\frac{1}{2}\left(1-\frac{1}{2a}\right)(2a-1)+\frac{1}{2}\left(1+\frac{1}{2a}\right)(2a+1)\\[1.5ex]
&=\frac{1}{2}\left(2a-1-1+\frac{1}{2a}+2a+1+1+\frac{1}{2a}\right)\\[1.5ex]
&=2a+\frac{1}{2a}
\end{align}
$$となる.
よって,$$
S= \begin{cases}
\displaystyle -2a-\frac{1}{2a} & \displaystyle \left(a\leq -\frac{1}{2} のとき\right) \\[1.5ex]
2 & \displaystyle \left(-\frac{1}{2} < a< \frac{1}{2} のとき\right) \\[1.5ex]
\displaystyle2a+\frac{1}{2a} & \displaystyle \left(a\geq \frac{1}{2} のとき\right)
\end{cases}
$$となる.
(2) \(S\)は\(a\)に関して偶関数となるので, \(a\geq 0\)の範囲で考える. \(\displaystyle a\geq \frac{1}{2}\)のとき, 相加相乗平均から$$
S=2a+\frac{1}{2a}\geq 2\sqrt{2a\cdot\frac{1}{2a}}=2
$$であり, \(\displaystyle a\geq \frac{1}{2}\)に注意して, 等号成立は,$$
\begin{align}
& 2a=\frac{1}{2a}\\[1.5ex]
\iff & a^2=\frac{1}{4}\\[1.5ex]
\iff & a=\frac{1}{2}\\[1.5ex]
\end{align}
$$のときである.
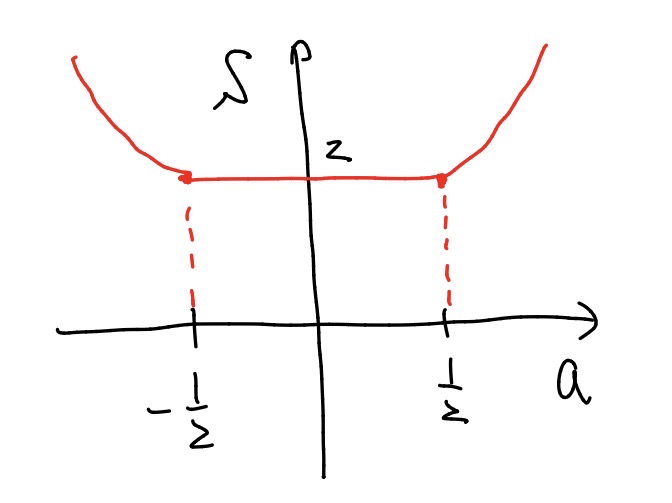
偶関数であることにも注意して, \(S(a)\)のグラフは以下のようになり, \(S(a)\)の最小値は\(2\)であることがわかる.
youtubeでも解説しています.








