高校数学問題を解きまくる– category –
-

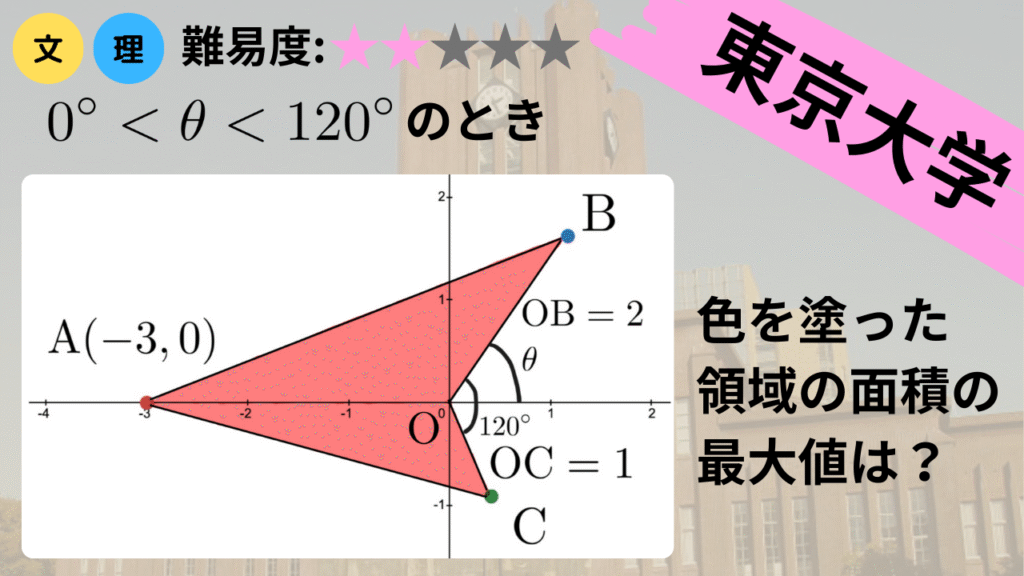
【東京大学 文系1 (2010)】三角関数と三角形の面積の最大化
-

【東京大学 文系1 (2010)】三角関数と三角形の面積の最大化
-

【東京大学 文系4 (2009)】絶対値が入る積分の場合分け
-

【東京大学入試】2箱に4色の玉が揃う確率を求める(2009)
-

【東京大学入試】二項係数の最大公約数と帰納法(2009)
-

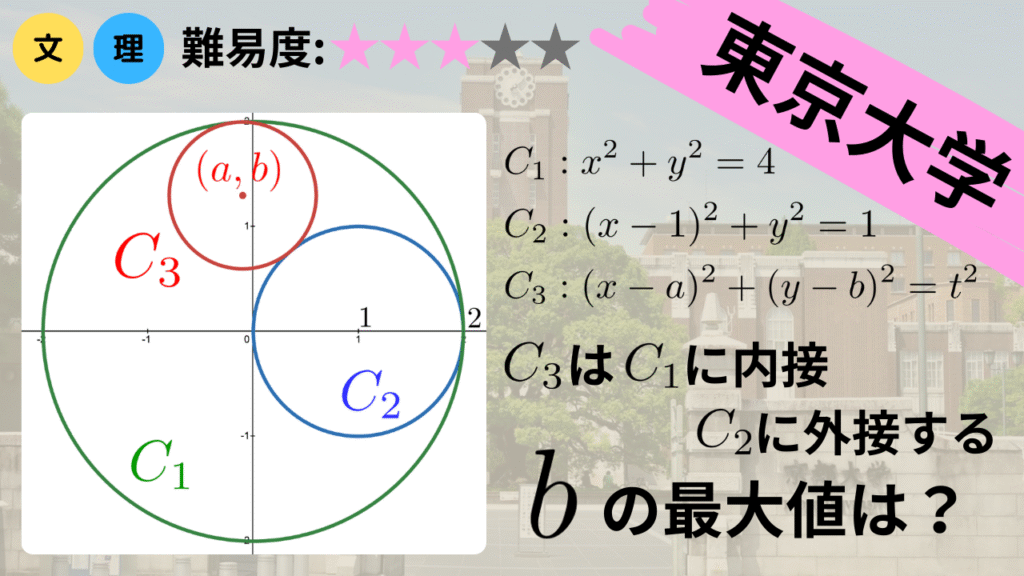
【東京大学入試】2つの円に内接・外接する円の中心と最大の高さ(2009)
-

【東京大学入試】漸化式と整数の融合問題(2008)
-

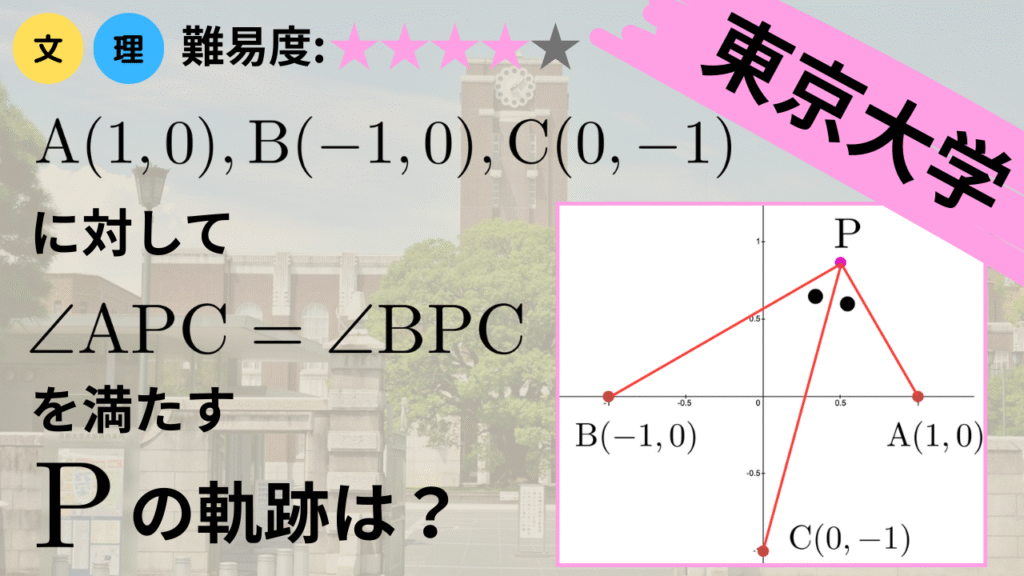
【東京大学入試】∠APC=∠BPCを満たす点Pの軌跡を求めよ!(2008)
-

【東京大学入試】カード入れ替えで初めて全同色になる確率を求める(2008)
-

【東京大学入試】定積分の条件から最大値を求める問題(2008)