今回はこちらの問題を解いていきます.
問1. 複素数\(z\)が\(|z|=2\)を満たす複素数全体を動くとき, \(\left|z-\frac{i}{z}\right|\)の最大値と最小値を求めよ.
問2. 以下の定積分の値を求めよ.
(1) \(\displaystyle \int_0^{\sqrt{3}}\frac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx\)
(2) \(\displaystyle\int_0^{\frac{\pi}{2}}\sqrt{\frac{1-\cos{x}}{1+\cos{x}}}dx\)
(2025 京都大学理系[1])
こちらは京都大学の理系の入試問題ですが, 小問集ということで難易度はそれほど高くありません. 最後に別解も紹介します.
それでは解いていきましょう.
問1
\(z\)の絶対値は\(2\)なので, 極形式で表すと\(z=2\left(\cos{\theta}+i\sin{\theta}\right)\)となり, \(\theta\)は\(0\leq \theta< 2\pi\)の範囲を動くと考えて良い. このとき, ド・モアブルの定理から,
$$
\begin{align}
\frac{1}{z}&=z^{-1}=\left\{2\left(\cos{\theta}+i\sin{\theta}\right)\right\}^{-1}\\[1.5ex]
&=\frac{1}{2}\left(\cos{(-\theta)}+i\sin{(-\theta)}\right)\\[1.5ex]
&=\frac{1}{2}\left(\cos{\theta}-i\sin{\theta}\right)
\end{align}
$$となる. よって,
$$
\begin{align}
\left|z-\frac{i}{z}\right|&=\left|2\left(\cos{\theta}+i\sin{\theta}\right)-i\cdot\frac{1}{2}\left(\cos{\theta}-i\sin{\theta}\right)\right|\\[1.5ex]
&=\left|\left(2\cos{\theta}-\frac{1}{2}\sin{\theta}\right)+i\left(2\sin{\theta}-\frac{1}{2}\cos{\theta}\right)\right|\\[1.5ex]
&=\sqrt{\left(2\cos{\theta}-\frac{1}{2}\sin{\theta}\right)^2+\left(2\sin{\theta}-\frac{1}{2}\cos{\theta}\right)^2}\\[1.5ex]
&=\sqrt{4\cos^2{\theta}-2\cos{\theta}\sin{\theta}+\frac{1}{4}\sin^2{\theta}+4\sin^2{\theta}-2\sin{\theta}\cos{\theta}+\frac{1}{4}\cos^2{\theta}}\\[1.5ex]
&=\sqrt{4-4\cos{\theta}\sin{\theta}+\frac{1}{4}}\\[1.5ex]
&=\sqrt{\frac{17}{4}-2\cdot 2\cos{\theta}\sin{\theta}}\\[1.5ex]
&=\sqrt{\frac{17}{4}-2\sin{2\theta}}\\
\end{align}
$$となる(途中の式変形では, \(\sin^2{\theta}+\cos^2{\theta}=1\)と, \(\sin\)の倍角の公式 \(\sin{2\theta}=2\sin{\theta}\cos{\theta}\)を用いた).
\(0\leq \theta < 2\pi\)のとき, \(0\leq 2\theta < 4\pi\)であり, \(\sin{2\theta}\)は\(-1\leq \sin{2\theta}\leq 1\)であるから, \(\sin{2\theta}=-1\), つまり\(\theta=\frac{3\pi}{4}, \frac{7\pi}{4}\)のとき, 最大値
$$
\sqrt{\frac{17}{4}+2}=\sqrt{\frac{25}{4}}=\frac{5}{2}
$$をとり, \(\sin{2\theta}=1\), つまり\(\theta=\frac{\pi}{4}, \frac{5\pi}{4}\)のとき, 最小値
$$
\sqrt{\frac{17}{4}-2}=\sqrt{\frac{9}{4}}=\frac{3}{2}
$$
をとることがわかる.
問2 (1)
被積分関数を分子の項ごとに分解すると,
$$
\begin{align}
\int_0^{\sqrt{3}}\frac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx &=\int_0^{\sqrt{3}}\frac{x\sqrt{x^2+1}}{x^2+1}dx\\[1.5ex]
&+\int_0^{\sqrt{3}}\frac{2x^3}{x^2+1}dx+\int_0^{\sqrt{3}}\frac{1}{x^2+1}dx
\end{align}
$$
となる. ここで2番目の積分は分子の次数が分母の次数以上になっているので割り算をして次数を下げる.
$$
\frac{2x^3}{x^2+1}=\frac{2x(x^2+1)-2x}{x^2+1}=2x-\frac{2x}{x^2+1}
$$
この結果を用いて2番目の積分の被積分関数を変形すると, 求めたい積分は以下の4つの積分に分解される.
$$
\begin{align}
\int_0^{\sqrt{3}}\frac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx &=\int_0^{\sqrt{3}}\frac{x\sqrt{x^2+1}}{x^2+1}dx\\[1.5ex]
&+\int_0^{\sqrt{3}}{2x}dx-\int_0^{\sqrt{3}}\frac{2x}{x^2+1}dx+\int_0^{\sqrt{3}}\frac{1}{x^2+1}dx
\end{align}
$$
これを1つずつ計算していく.
① 1番目の積分
分母分子を\(\sqrt{x^2+1}\)で割ると, 以下の形になる.
$$
\int_0^{\sqrt{3}}\frac{x\sqrt{x^2+1}}{x^2+1}dx=\int_0^{\sqrt{3}}\frac{x}{\sqrt{x^2+1}}dx
$$ \(t=x^2+1\)とおくと, 積分範囲は,
$$
\begin{array}{c|ccc}
x & 0 & \rightarrow & \sqrt{3} \\
\hline
t & 1 & \rightarrow & 4 \\
\end{array}
$$となり, \(dt=2xdx\)より, \(xdx=\frac{1}{2}dt\)となるので, 置換積分を実行して,
$$
\begin{align}
\int_0^{\sqrt{3}}\frac{x}{\sqrt{x^2+1}}dx&=\frac{1}{2}\int_1^3\frac{1}{\sqrt{t}}dt\\
&=\frac{1}{2}\left[2\sqrt{t}\right]_1^3=\sqrt{4}-\sqrt{1}=1
\end{align}
$$となる.
② 2番目の積分
$$
\int_0^{\sqrt{3}}2xdx=\left[x^2\right]_0^\sqrt{3}=3
$$
③ 3番目の積分
分子が分母を微分した形になっているので, 以下のように計算ができる(慣れていない方は, \(t=x^2+1\)と置換して置換積分で計算しても良い).
$$
\begin{align}
\int_0^{\sqrt{3}}\frac{2x}{x^2+1}dx&=\int_0^{\sqrt{3}}\frac{\left(x^2+1\right)^{\prime}}{x^2+1}dx\\[1.5ex]
&=\left[\log{|x^2+1|}\right]_0^\sqrt{3}=\log{4}-\log{1}=2\log{2}
\end{align}
$$
④ 4番目の積分
\(x=\tan{\theta}\)とおくと, 積分範囲は,
$$
\begin{array}{c|ccc}
x & 0 & \rightarrow & \sqrt{3} \\
\hline
\theta & 0 & \rightarrow & \frac{\pi}{3} \\
\end{array}
$$となり, \(dx=\frac{1}{\cos^2{\theta}}d\theta\)より, 置換積分を実行して,
$$
\begin{align}
\int_0^{\sqrt{3}}\frac{1}{x^2+1}dx&=\int_0^{\frac{\pi}{3}}\frac{1}{\tan^2{\theta}+1}\frac{1}{\cos^2{\theta}}d\theta\\[1.5ex]
&=\int_0^{\frac{\pi}{3}}d\theta=\frac{\pi}{3}
\end{align}
$$となる(\((\tan^2{\theta}+1)\cdot\cos^2{\theta}=1\)に注意).
①から④より求めるべき積分の値は,
$$
\begin{align}
\int_0^{\sqrt{3}}\frac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx &=1+3-2\log{2}+\frac{\pi}{3}=4-2\log{2}+\frac{\pi}{3}
\end{align}
$$と求まる.
問2 (2)
以下の半角の公式から,
$$
\begin{align}
\cos^2{\frac{x}{2}}&=\frac{1+\cos{x}}{2}\\[1.5ex]
\sin^2{\frac{x}{2}}&=\frac{1-\cos{x}}{2}
\end{align}
$$\(1+\cos{x}\), \(1-\cos{x}\)は以下のように変形できる.
$$
\begin{align}
1+\cos{x}&=2\cos^2{\frac{x}{2}}\\[1.5ex]
1-\cos{x}&=2\sin^2{\frac{x}{2}}\\
\end{align}
$$
今考えている積分範囲\(0\leq x\leq\frac{\pi}{2}\)では, \(\sin{\frac{x}{2}}\geq 0\), \(\cos{\frac{x}{2}}\geq 0\)であるから, \(\sqrt{\sin^2{\frac{x}{2}}}=\sin{\frac{x}{2}}\), \(\sqrt{\cos^2{\frac{x}{2}}}=\cos{\frac{x}{2}}\)となることに注意して, 被積分関数を変形していくと,
$$
\begin{align}
\int_0^{\frac{\pi}{2}} \sqrt{\frac{1 – \cos{x}}{1 + \cos{x}}} dx&= \int_0^{\frac{\pi}{2}} \sqrt{\frac{2\sin^2{\frac{x}{2}}}{2\cos^2{\frac{x}{2}}}} dx\\[1.5ex]
&= \int_0^{\frac{\pi}{2}} \sqrt{\frac{\sin^2{\frac{x}{2}}}{\cos^2{\frac{x}{2}}}} dx = \int_0^{\frac{\pi}{2}} \frac{\sin{\frac{x}{2}}}{\cos{\frac{x}{2}}} dx
\end{align}
$$ となります. ここで,
$$
\left(\cos{\frac{x}{2}}\right)^{\prime}=-\frac{1}{2}\sin{\frac{x}{2}}
$$より,
$$
\sin{\frac{x}{2}}=-2\left(\cos{\frac{x}{2}}\right)^{\prime}
$$であるので, 積分の計算を続けると,
$$
\begin{align}
\int_0^{\frac{\pi}{2}} \sqrt{\frac{1 – \cos{x}}{1 + \cos{x}}} dx&=\int_0^{\frac{\pi}{2}} \frac{\sin{\frac{x}{2}}}{\cos{\frac{x}{2}}} dx\\[1.5ex]
&=-2\int_0^{\frac{\pi}{2}} \frac{\left(\cos{\frac{x}{2}}\right)^{\prime}}{\cos{\frac{x}{2}}} dx\\[1.5ex]
&=-2\left[\log{\left|\cos{\frac{x}{2}}\right|}\right]_0^{\frac{\pi}{2}}\\[1.5ex]
&=-2\left(\log{\frac{1}{\sqrt{2}}}-\log{1}\right)=\log{2}
\end{align}
$$となる.
いくつか注意点です. この解答でも何度か使っていますが, 分子が分母を微分した形になっている分数の関数を積分すると\(\log{(分母)}\)になります. これが使えると余計な置換操作が減るので是非使いこなしたいところです.
$$
\int\frac{\left(f(x)\right)^\prime}{f(x)}dx=\log{f(x)}+C
$$
また, \(\frac{1}{\sqrt{t}}\)の積分は, \(\frac{1}{\sqrt{t}}=t^{-\frac{1}{2}}\)より,
$$
\int{x^{\alpha}}dx=\frac{x^{\alpha + 1}}{\alpha + 1}+C
$$
を用いて,
$$
\int{t^{-\frac{1}{2}}}dt=\frac{t^{-\frac{1}{2} + 1}}{-\frac{1}{2}+ 1}+C=2t^{-\frac{1}{2}}+C
$$より求まります.
最後に問1の別解を2つ, 問2(2)の別解を1つ紹介します.
問1(別解1)
\(|z|=2\)より,
$$
\left|z-\frac{1}{z}\right|=\left|\frac{z^2-i}{z}\right|=\frac{\left|z^2-i\right|}{\left|z\right|}=\frac{1}{2}\left|z^2-i\right|
$$となる.
ここで\(z=2(\cos{\theta}+i\sin{\theta}\)とすると, ド・モアブルの定理から, \(z^2=4(\cos{2\theta}+i\sin{2\theta})\)なので, 続きを計算すると,
$$
\begin{align}
\frac{1}{2}\left|z^2-i\right|&=\frac{1}{2}\left|4\cos{2\theta}+i\left(4\sin{2\theta}-1\right)\right|\\[1.5ex]
&=\frac{1}{2}\sqrt{\left(4\cos{2\theta}\right)^2+\left(4\sin{2\theta}-1\right)^2}\\[1.5ex]
&=\frac{1}{2}\sqrt{16\cos^2{2\theta}+16\sin^2{2\theta}-8\sin{2\theta}+1}\\[1.5ex]
&=\frac{1}{2}\sqrt{17-8\sin{2\theta}}\\
\end{align}
$$となります.
\(0\leq \theta < 2\pi\)のとき, \(0\leq 2\theta < 4\pi\)であり, \(\sin{2\theta}\)は\(-1\leq \sin{2\theta}\leq 1\)であるから, \(\sin{2\theta}=-1\), つまり\(\theta=\frac{3\pi}{4}, \frac{7\pi}{4}\)のとき, 最大値
$$
\frac{1}{2}\sqrt{17+8}=\frac{5}{2}
$$をとり, \(\sin{2\theta}=1\), つまり\(\theta=\frac{\pi}{4}, \frac{5\pi}{4}\)のとき, 最小値
$$
\frac{1}{2}\sqrt{17-8}=\frac{3}{2}
$$
をとることがわかる.
問1(別解2)
\(|z|=2\)より,
$$
\left|z-\frac{1}{z}\right|=\left|\frac{z^2-i}{z}\right|=\frac{\left|z^2-i\right|}{\left|z\right|}=\frac{1}{2}\left|z^2-i\right|
$$となる.
ここで, \(\left|z^2-i\right|\)は複素数平面上で\(z^2\)と\(i\)の距離である. ここで\(z=2(\cos{\theta}+i\sin{\theta}\)とすると, ド・モアブルの定理から, \(z^2=4(\cos{2\theta}+i\sin{2\theta})\)となり, \(\left|z^2\right|\)は複素数平面上で原点(\0\)を中心とする半径\(4\)の円周上を(くまなく)動く.
2つの円が内接するとき, その接点と2つの中心が1直線上になることを考慮すれば, 点\(i\)と円周上の点の距離の最小値, 最大値はそれぞれ\(3\), \(5\)となる. 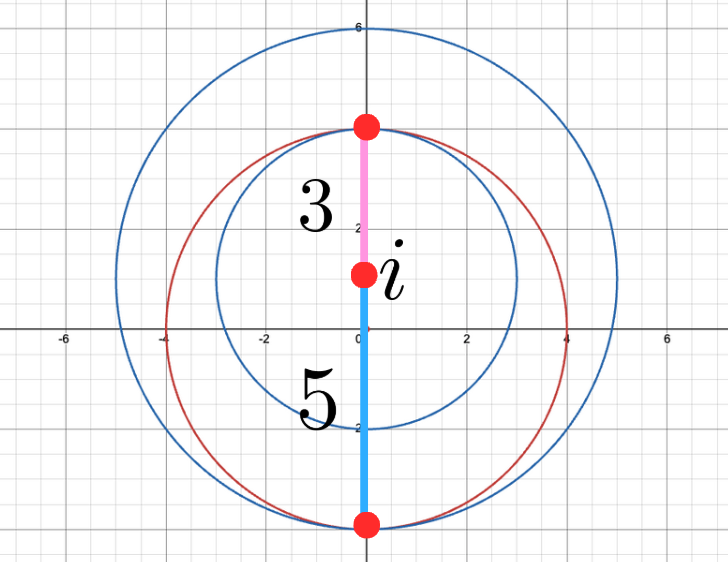
よって, これを\(\frac{1}{2}\)倍した\(\frac{3}{2}\), \(\frac{5}{2}\)がそれぞれ最小値, 最大値となる.
この問1(別解2)のように図形的な意味も考えながら問題を解くと今後解ける問題の幅が広がるでしょう.
最後に問2(2)の別解です. これは上の解答であった半角の公式を使った変換が思いつかない方向けの解答です.
問2(2)(別解)
$$
\int_0^{\frac{\pi}{2}}\sqrt{\frac{1-\cos{x}}{1+\cos{x}}}dx
$$
にて, \(t=\cos{x}\)とおくと, 積分範囲は,
$$
\begin{array}{c|ccc}
x & 0 & \rightarrow & \frac{\pi}{2} \\
\hline
t & 1 & \rightarrow & 0 \\
\end{array}
$$となる. また, \(dt=-\sin{x}dx\)であるが, 今考えている積分範囲\(0\leq x\leq \frac{\pi}{2}\)では, \(\sin{x}\geq 0\)より,
$$
\sin{x}=\sqrt{1-\cos^2{x}}
$$
である, ここで, \(\cos{x}=t\)より,
$$
dt=-\sin{x}dx=-\sqrt{1-\cos^2{x}}dx=-\sqrt{1-t^2}dx
$$であるから,
$$
dx=-\frac{1}{\sqrt{1-t^2}}dt
$$となり, \(dx\)を\(dt\)に変換できる.
以上から, 置換積分を行うと,
$$
\begin{align}
\int_0^{\frac{\pi}{2}}\sqrt{\frac{1-\cos{x}}{1+\cos{x}}}dx&=\int_1^0\sqrt{\frac{1-t}{1+t}}\left(-\frac{1}{\sqrt{1-t^2}}\right)dt\\[1.5ex]
&=\int_0^1\frac{\sqrt{1-t}}{\sqrt{{1+t}}}\frac{1}{\sqrt{1-t}\sqrt{1+t}}dt\\[1.5ex]
&=\int_0^1\frac{1}{1+t}dt\\
\end{align}
$$である(途中で, \(-(マイナス)\)を使って積分区間の上端と下端を交換している)ことに注意.
この積分は分子が分母を微分した形になっているので,
$$
\int_0^1\frac{1}{1+t}dt=\left[\log{1+t}\right]_0^1=\log{2}
$$となる.
youtubeでも解説しています.