今回はこちらの問題を解いていきます.
\(\triangle{ABC}\)に関して, \(\tan{A}\), \(\tan{B}\), \(\tan{C}\)がすべて整数であるとき, その値を求めよ. (1984 一橋大学)
一橋大学は整数問題の良問が多く, こちらも図形問題に見えますが, 実は整数問題です. \(\tan\)はどんな整数の値を取ることができるので, 答えも無限にありそうですが, \(A, B, C\)は三角形の3つの角ということで, その関係式から答えは1つになります.
では解答に参りましょう.
\(A\leq B \leq C\)としても一般性を失わない.
\(A, B, C\)は三角形の3つの角だから, \(A + B + C = 180\,^\circ\)である. この関係式と先の不等式より, $$
180\,^\circ = A+B+C \geq A+A+A=3A
$$となり, 両辺を3で割ることで, \(A\geq 60\,^\circ\)であることがわかる.
ここで, 角度が\(0\,^\circ\)から\(90\,^\circ\)の間で\(\tan\)のグラフを考える.
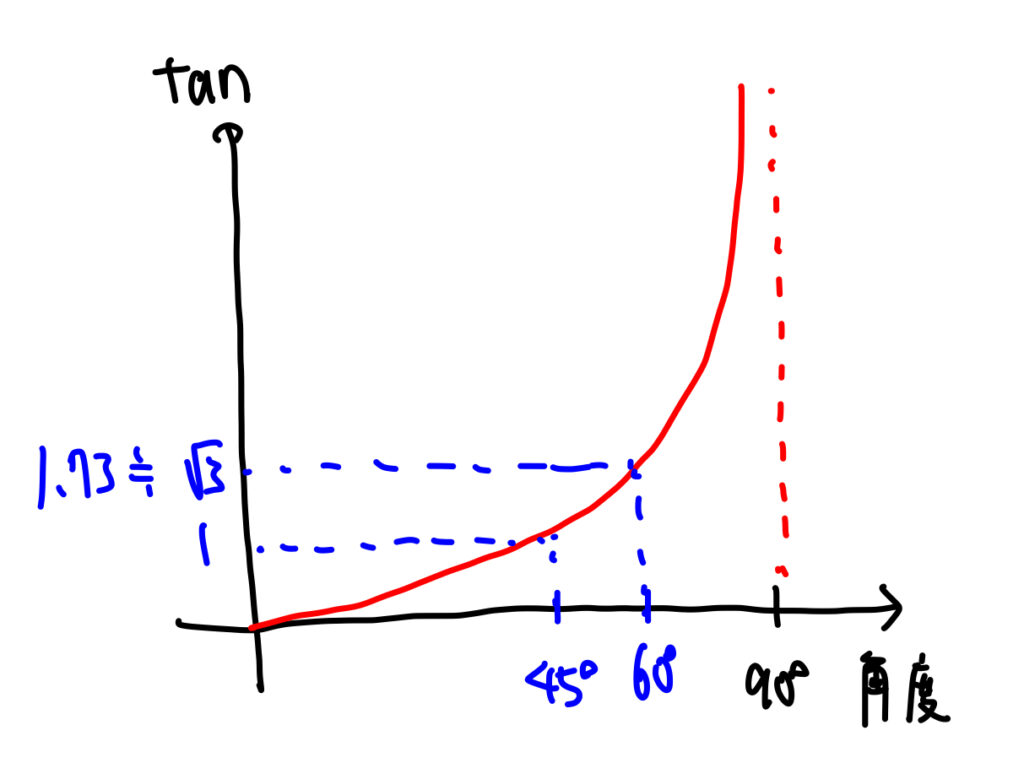
この範囲では角度が大きくなるにつれて\(\tan\)の値は大きくなる(このような関数の性質を単調増加と言います). \(A\)は\(0\,^\circ\)より大きく, \(60\,^\circ\)以下であることがわかっており, \(\tan{60\,^\circ}=\sqrt{3}\)で\(\sqrt{3}= 1.73\cdots \)は\(2\)より小さいため, この範囲で\(\tan{A}\)が整数となるのは\(A=45\,^\circ\)の時のみで, \(\tan{A}=1\)となる.
\(A=45\,^\circ\)と決まったので, \(A+B+C=180\,^\circ\)より, \(B+C=135\,^\circ\)であることがわかり, このことから以下のようにして\(\triangle{ABC}\)は鋭角三角形であることが言える.
\(A\leq B\)より, \(B\geq 45\,^\circ\)である. \(135\,^\circ =B+C\leq 45\,^\circ + C\)より, \(C\leq 90\,^\circ\)となるが, 問題の大前提より, \(\tan{C}\)は整数である必要があり, \(C\neq 90\,^\circ\)が得られる. よって, \(\triangle{ABC}\)の最大角\(C\)は\(C<90\,^\circ\)であることがわかり, \(\triangle{ABC}\)は鋭角三角形となる.
以上から, \(45\,^\circ\leq B\leq C < 90\,^\circ\)となり, この範囲での\(\tan\)のグラフより, \(\tan{B}\), \(\tan{C}\)に関する不等式, $$1\leq \tan{B}\leq \tan{C}$$が得られる.
次に, \(\tan{(B+C)}=\tan{135\,^\circ}=-1\)であるが, これに\(\tan\)の加法定理を用いると, $$\frac{\tan{B}+\tan{C}}{1-\tan{B}\tan{C}}=-1$$となり, これを整理すると, $$\tan{B}\tan{C}-\tan{B}-\tan{C}-1=0$$を得る. これを以下のように変形すると, $$(\tan{B}-1)(\tan{C}-1)=2$$となり, \(\tan{B}-1\)も\(\tan{C}-1\)も整数であり, また, $$1\leq \tan{B}\leq \tan{C}$$であることから, \(0<\tan{B}-1\leq \tan{C}-1\)であるので, \(\tan{B}-1=1\), \(\tan{C}-1=2\)のみが許され, \(\tan{B}=2\), \(\tan{C}=3\)となる.
先に得ていた\(\tan{A}=1\)も加えて, $$\tan{A}=1, \tan{B}=2, \tan{C}=3$$が答えとなる.
上の解答で, \(A\)は\(45\,^\circ\)であることはわかりますが, \(B\)と\(C\)の角度は整数にならず簡単には書き表せません. 大学数学では\(\arctan\)という関数を使うことで, \(B=\arctan{2}\), \(C=\arctan{3}\)と一応記述することはできますが, これらは特に新しい情報を与えるものではありません.
関数電卓などを用いると\(B\), \(C\)の近似値を得ることができて, 計算すると\(B=63.43\cdots\,^\circ\), \(C=71.57\cdots\,^\circ\)となり, たしかに\(A+B+C=180\,^\circ\)を満たしそうであることがわかります.
youtubeでも解説しています.








