今回はこちらの問題を解いていきます.
\(\alpha\)を\(xyz\)空間内の3点\(A(1,1,-5), B(-1,-1,7), C(1,-1,3)\)を通る平面とし. 点\(P(a,b,t)\)を通り\(\alpha\)に垂直な直線と, \(xy\)平面との交点を\(Q\)とする.
(1) 点\(Q\)の座標を求めよ.
(2) \(t\)を実数全体で動かすとき, \(OQ\)の最小値が\(1\)以下となるような\(a, b\)の条件を求めよ.
(2025 九州大学理系[1])
平面に垂直な直線は, その方向ベクトルが平面上の\(\overrightarrow{0}\)でない任意のベクトルと直交します. ここではこの性質を用いて問題を解いていきます.
図形問題は図形を描いた方がよいのですが, 今回の問題のように3次元の座標空間内に平面を描くのは難しいため, 座標は気にせずざっくり意味がわかる図を描いておきます.
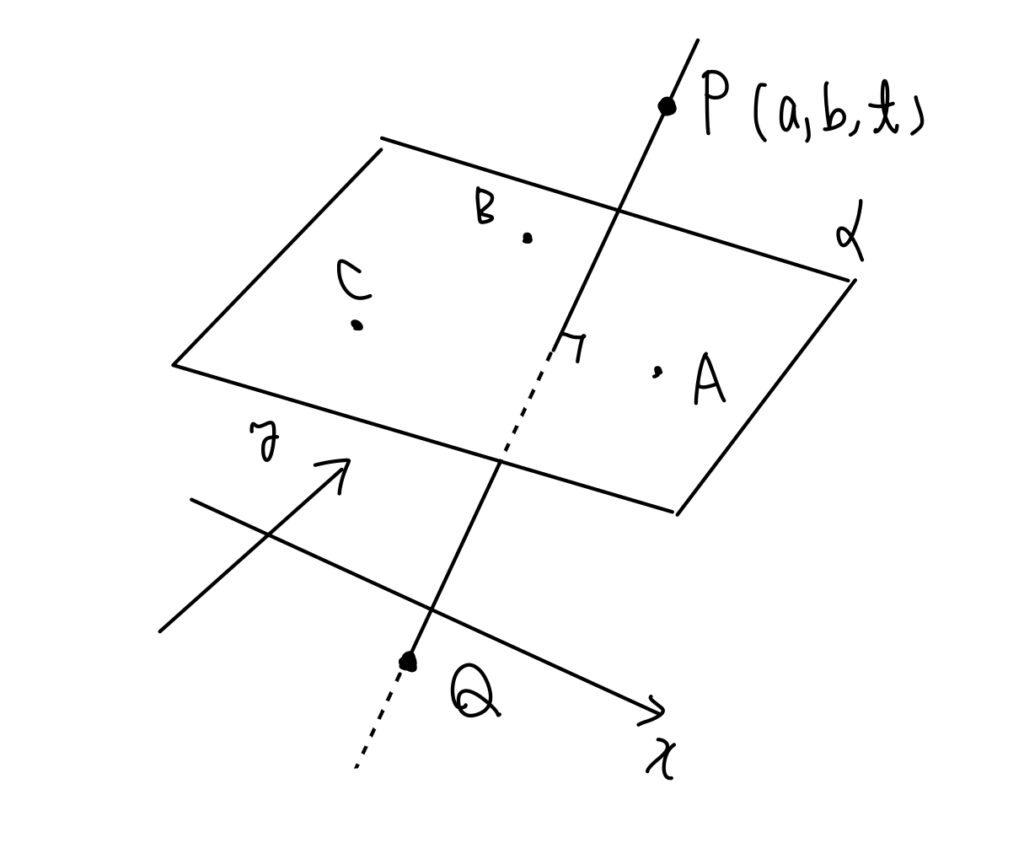
要は, 平面\(\alpha\)上に\(A, B, C\)があって, 空間内の点\(P\)から平面\(\alpha\)に垂線を下ろします. 平面\(\alpha\)が\(yz\)平面に対して傾いているため, その垂線を延長すると必ず\(xy\)平面にぶつかります. その交点を\(Q\)としています. この図を念頭に置いて, 問題を解いていきましょう.
(1) \(Q\)は\(xy\)平面上の点なので, \((x,y,0)\)とおける. また, \(\overrightarrow{PQ}\)は平面\(\alpha\)に垂直だから, 平面\(\alpha\)上のベクトル \(\overrightarrow{AB}\), \(\overrightarrow{AC}\)と垂直である. これから,
$$
\begin{align}
\overrightarrow{PQ}\cdot\overrightarrow{AB}=0\\
\overrightarrow{PQ}\cdot\overrightarrow{AC}=0
\end{align}
$$
が成り立つことがわかる.
ここで, \(\overrightarrow{PQ}\), \(\overrightarrow{AB}\), \(\overrightarrow{AC}\)を成分表示すると,
$$
\begin{align}
\overrightarrow{PQ}&=(x,y,0)-(a,b,t)=(x-a,y-b,-t)\\
\overrightarrow{AB}&=(-1,-1,7)-(1,1,-5)=(-2,-2,12)\\
\overrightarrow{AC}&=(1,-1,3)-(1,1,-5)=(0,-2,8)
\end{align}
$$
となるので, 先の内積\(0\)の条件式に代入して,
$$
\begin{align}
(x-a,y-b,-t)\cdot(-2,-2,12)&=-2(x-a)-2(y-b)-12t=0\\
(x-a,y-b,-t)\cdot(0,-2,8)&=-2(y-b)-8t=0
\end{align}
$$
を得る. これを\(x\), \(y\)について解けばよい. 2番目の条件式から,
$$
y=b-4t
$$
がわかり, これを1番目の式に代入して,
$$
x=a-2t
$$
がわかる.
よって\(Q\)の座標は\((a-2t,b-4t,0)\)となる.
(2) \(OQ\geq 0\)より, \(OQ\)の最小値が\(1\)以下であることと, \(OQ^2\)の最小値が\(1\)以下であることは同値である.
$$
OQ^2=(a-2t)^2+(b-4t)^2=20t^2-(4a+8b)t+a^2+b^2
$$
となる. これは\(t\)の2次関数となり, \(t\)がすべての実数値をうごくことと, \(t^2\)の係数が\(20\)で正であることから, 平方完成することで最小値がわかる.
実際に\(OQ^2\)を平方完成すると,
$$
OQ^2=20t^2-(4a+8b)t+a^2+b^2=20\left(t-\frac{a+2b}{10}\right)^2+\frac{(2a-b)^2}{5}
$$
となり, \(t=\frac{a+2b}{10}\)のとき, \(OQ^2\)は最小値\(\frac{(2a-b)^2}{5}\)をとることがわかる.
この最小値が\(1\)以下ということから,
$$
\frac{(2a-b)^2}{5}\leq 1 \iff (2a-b)^2\leq 5 \iff -\sqrt{5}\leq 2a-b\leq\sqrt{5}
$$
が求めるべき\(a, b\)の条件である.
平方完成をしている部分は, \(OQ^2\)を\(t\)で微分して, 最小値をとる\(t\)を求めてから\(OQ^2\)の式に代入することで最小値を求めても構いません. いずれにしてもそれなりの計算になるため, 今回は平方完成で最小値を導出しました.
グラフを書けばすぐわかることですが, \(a>0\)に対して
$$
\begin{align}
x^2<a &\iff -\sqrt{a}<x<\sqrt{a}\\
x^2>a &\iff x<-\sqrt{a} ,\,\, x>\sqrt{a}
\end{align}
$$
などはすぐに使えるようにしておきましょう.
youtubeでも解説しています.
