今回はこちらの問題を解いていきます.
(1) \(t=x+\frac{1}{x}\) \((x\neq 0\)とするとき, \(x^2+x-10+\frac{1}{x}+\frac{1}{x^2}\)を\(t\)の式で表せ.
(2) 4次方程式\(x^4+x^3-10x^2+x+1=0\)を解け.
(2025 東京都立大学)
2次方程式は解の公式で解けますが, 3次方程式, 4次方程式など高次元の方程式については, その解の公式を高校では学ばないため, 簡単には解けません. しかも, 5次方程式以降は解の公式が存在しないことが証明されています. これは大学でガロア理論を学ぶことで理解ができます. また, 3次方程式, 4次方程式の解の公式は存在はしますが, その形はとても複雑で解の公式を使うことを前提とする入試問題は出てきません. 高校レベルの数学で高次方程式を解く典型的な方法は, 具体的に解を見つけて, 方程式の次数を下げていくものです.
今回の問題は最終的には4次方程式を解く問題ですが, 具体的に解を見つけることが困難です. 今回は4次方程式の係数に対称性がある場合の典型的解法を用いて解いていきます. ここでいう対称性は以下のように\(x^4\)の係数と定数項, \(x^3\)と\(x\)の係数がそれぞれ等しいことを言います.
$$
ax^4+bx^3+cx^2+bx+a=0
$$
x^2を中心として係数が線対象に並んでいるように見えるので対称性という表現を用いています.
このような形をした4次方程式は,
$$
t=x+\frac{1}{x}
$$
を用いて\(t\)の2次方程式に変換することで解くことができます.
では実際の問題を解いてその解法を会得しましょう.
(1) \(t=x+\frac{1}{x}\)の両辺を2乗すると,
$$
t^2=x^2+2x\cdot\frac{1}{x}+\left(\frac{1}{x}\right)^2=x^2+\frac{1}{x^2}+2
$$
となり, これから,
$$
x^2+\frac{1}{x^2}=t^2-2
$$
となるので,
$$
\begin{align}
x^2+x-10+\frac{1}{x}+\frac{1}{x^2}&=(x^2+\frac{1}{x^2})+(x+\frac{1}{x})-10\\[1.5ex]
=&t^2-2+t-10=t^2+t-12
\end{align}
$$と表せる.
(2) \(x^4+x^3-10x^2+x+1=0\)において, \(x=0\)はこの解ではないから以降\(x\neq 0\)とする. \(x^2\neq 0\)より, 方程式の両辺を\(x^2\)で割ると,
$$
x^2+x-10+\frac{1}{x}+\frac{1}{x^2}=0
$$ となる. (1)より, \(t=x+\frac{1}{x}\)とおくと, これは
$$
t^2+t-12=0
$$
となる. この左辺は簡単に因数分解でき以下の形となるため,
$$
(t+4)(t-3)=0
$$
この解は\(t=3\)と\(t=-4\)となる. 各場合において対応する\(x\)を求める.
\(t=3\)のとき,
$$
x+\frac{1}{x}=3
$$
より,
$$
x^2-3x+1=0
$$
解の公式でこれを解いて,
$$
x=\frac{3\pm\sqrt{5}}{2}
$$
が得られる.
次に, \(t=-4\)のとき,
$$
x+\frac{1}{x}=-4
$$
より,
$$
x^2+4x+1=0
$$
解の公式でこれを解いて,
$$
x=-2\pm\sqrt{3}
$$
が得られる.
よって, 与えられた4次方程式の解は以下の4つである.
$$
x=\frac{3\pm\sqrt{5}}{2}, -2\pm\sqrt{3}
$$
4次関数\(y=x^4+x^3-10x^2+x+1\)のグラフを書くと以下のようになり, このグラフと\(x\)軸との交点の\(x\)座標が4次方程式\(x^4+x^3-10x^2+x+1=0\)の解に一致します.
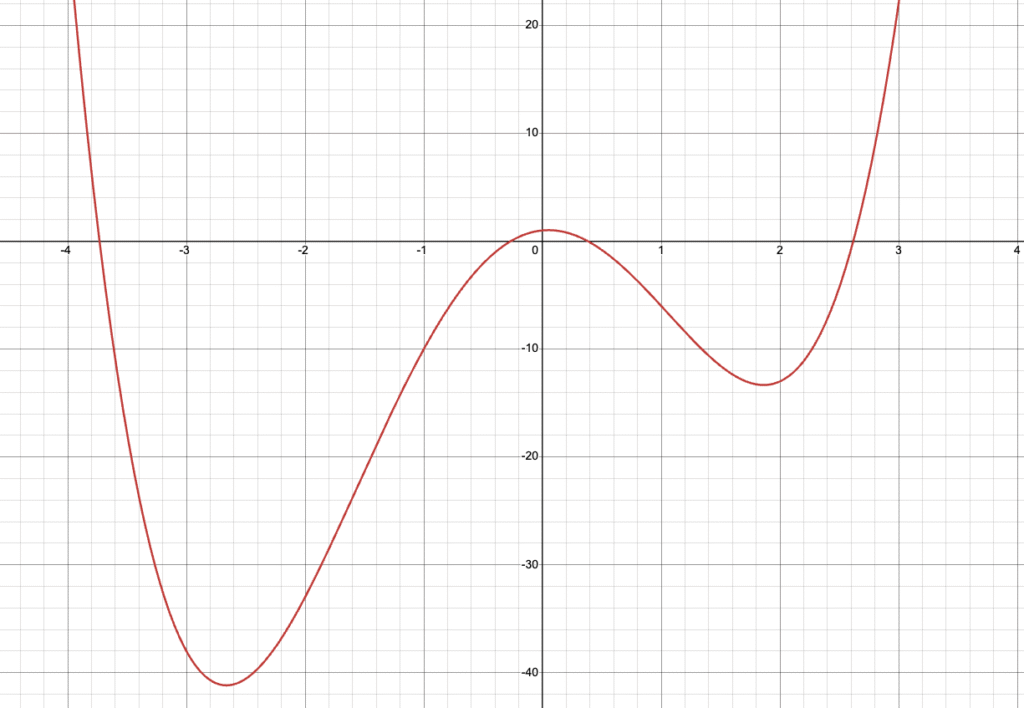
実際今回得られた4つの解は,
$$
\begin{align}
\frac{3+\sqrt{5}}{2}&=2.618\cdots\\[1.5ex]
\frac{3-\sqrt{5}}{2}&=0.381\cdots\\[1.5ex]
-2+\sqrt{3}&=-0.267\cdots\\[1.5ex]
-2-\sqrt{3}&=-3.732\cdots
\end{align}
$$
となり, たしかに上のグラフと\(x\)軸の交点の\(x\)座標に一致していることがわかります.
youtubeでも解説しています.








