今回はこちらの問題を解いていきます.
\(a\)を実数として, 関数\(f(x)\)を
\begin{equation} f(x)=\frac{1}{4}\left(\log_{\frac{1}{2}}{x^2}\right)^2-\log_{\frac{1}{2}}{\left(8x^{1-a}\right)}+a-8 \end{equation}
とする. \(\displaystyle t=\log_{\frac{1}{2}}{x}\)とおくとき, 以下の問いに答えよ.
(1) \(f(x)\)を\(t\)を用いて表せ.
(2) \(1\leq x\leq 4\)のとき, \(t\)の値の範囲を求めよ.
(3) 条件「\(1\leq x\leq 4\)のとき, \(f(x)<0\)である」を満たす\(a\)の値の範囲を求めよ.
(2020 東京都立大学 文系 [1])
それでは解いていきましょう.
(1) 一般に\(a>1\), \(x<0\)のとき, \(x^{1-a}\)は定義されないので, 真数条件と合わせて\(f(x)\)の定義域\(x>0\)である. \(x>0\)なので, \(\displaystyle \log_{\frac{1}{2}}{x^2}=2\log_{\frac{1}{2}}{x}\), \(\displaystyle \log_{\frac{1}{2}}{x^{1-a}}=(1-a)\log_{\frac{1}{2}}{x}\)であるから, $$
\begin{align}
f(x)&=\frac{1}{4}\left(2\log_{\frac{1}{2}}{x}\right)^2-\log_{\frac{1}{2}}{8}-(1-a)\log_{\frac{1}{2}}{x}+a-8\\[1.5ex]
&=t^2-(-3)-(1-a)t+a-8\\[1.5ex]
&=t^2-(1-a)t+a-5
\end{align}
$$となる.
(2) \(t=\log_{\frac{1}{2}}{x}\)のグラフから, \(1\leq x\leq 4\)のとき, \(-2\leq t\leq 0\)である.
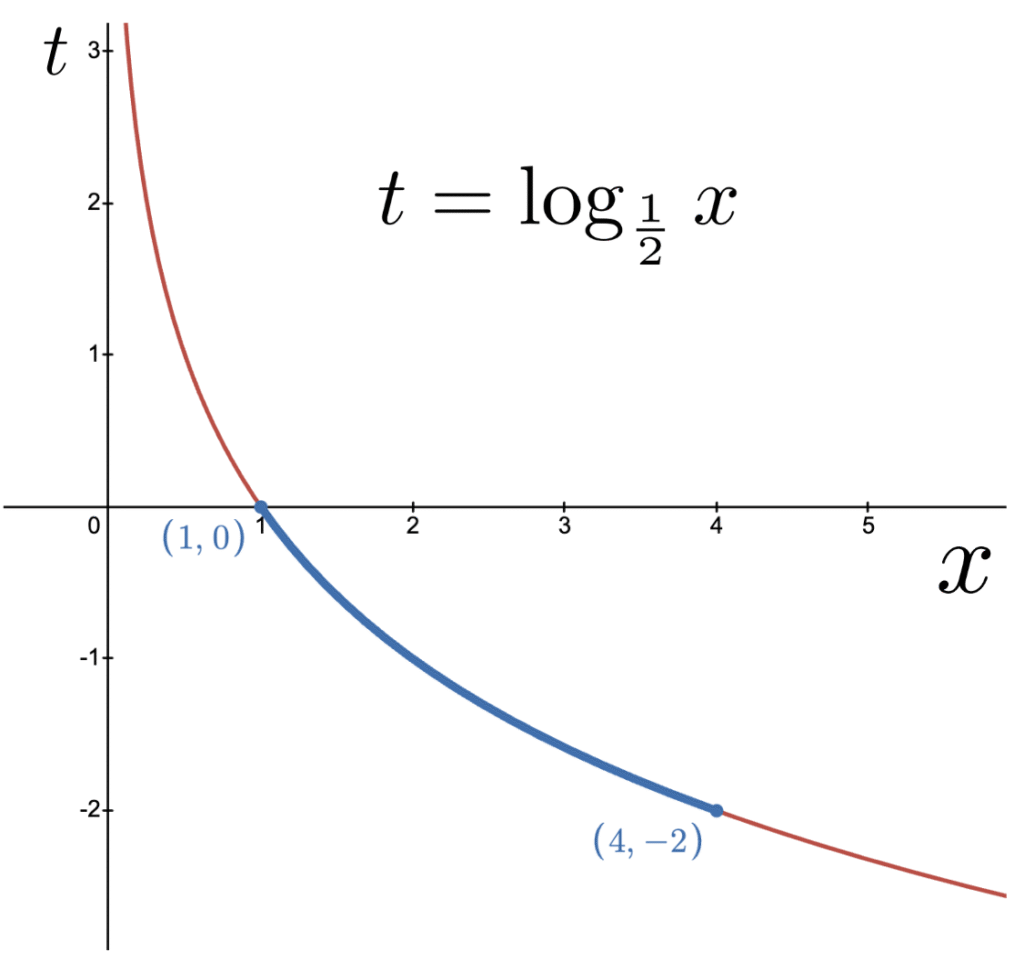
(3) \(g(t)=t^2-(1-a)t+a-5\)とおくと, (1), (2)より, 条件は「\(-2\leq t\leq 0\)のとき, \(g(t)<0\)である」と同値である. \(y=g(t)\)は下に凸の放物線のため, これは, 「\(g(-2)<0\) かつ \(g(0)<0\)」と同値である. $$
\begin{align}
g(-2)&=4+2(1-a)+a-5<0\\[1.5ex]
&\iff a>1\\[1.5ex]
g(0)&=a-5<0\\[1.5ex]
&\iff a<5
\end{align} より, 求める\(a\)の範囲は\(1<a<5\)となる.
youtubeでも解説しています.








