【千葉大学入試】最大角120°の三角形で余弦の値を求める(2014)

図のように, \(a=\mathrm{BC}\), \(b=\mathrm{CA}\), \(c=\mathrm{AB}\)とおく.

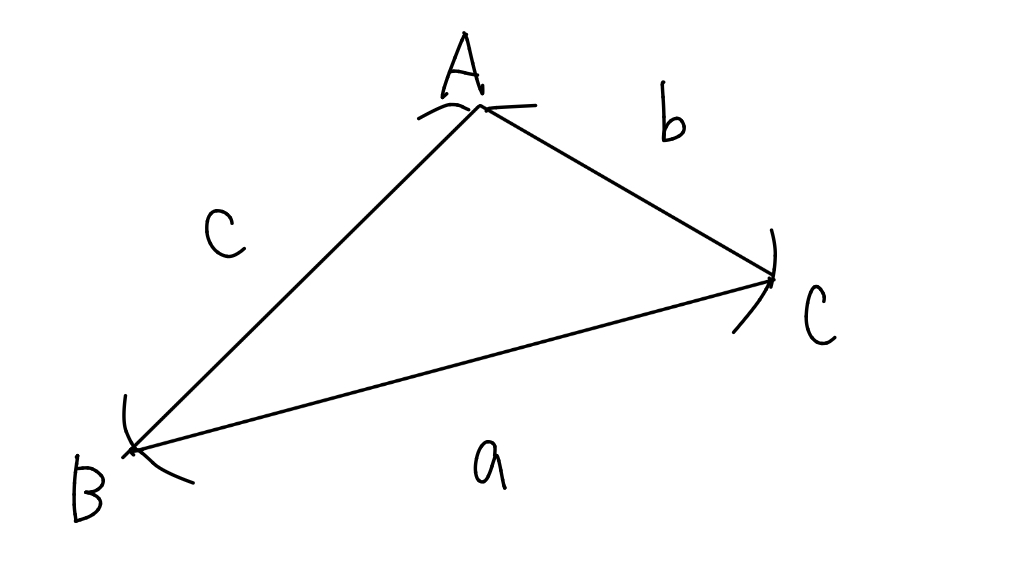
\(\triangle{\mathrm{ABC}}\)で正弦定理より,$$
\frac{a}{\sin{\mathrm{A}}}=\frac{b}{\sin{\mathrm{B}}}
$$となり, \(\displaystyle \frac{\sin{\mathrm{A}}}{5}=\frac{\sin{\mathrm{B}}}{3}\)と辺々をかけて,$$
\begin{align}
\frac{a}{\sin{\mathrm{A}}}\cdot \frac{\sin{\mathrm{A}}}{5}&=\frac{b}{\sin{\mathrm{B}}}\cdot\frac{\sin{\mathrm{B}}}{3}\\[1.5ex]
\frac{a}{5}&=\frac{b}{3}
\end{align}
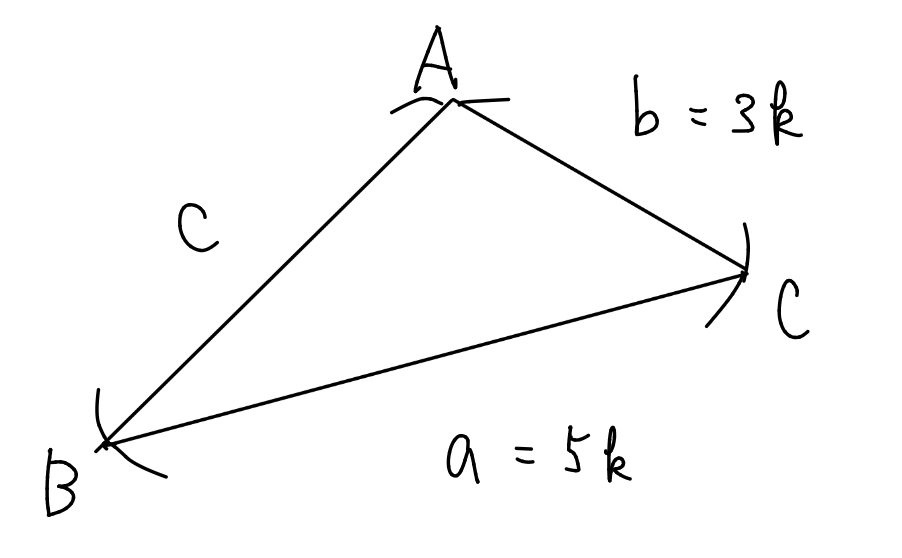
$$がわかる. \(\displaystyle \frac{a}{5}=\frac{b}{3}=k\)とおくと, \(k\)は正の実数であり, $$
\begin{align}
a&=5k\\[1.5ex]
b&=3k
\end{align}
$$となる.

ここで,\(\sin{\mathrm{B}}>0\)であることから,$$
\sin{\mathrm{A}}=\frac{5}{3}\sin{\mathrm{B}}>\sin{\mathrm{B}}
$$であり, 一般に, \(\triangle{\mathrm{ABC}}\)においては, 角\(\mathrm{A}\), \(\mathrm{B}\)の大小関係と, \(\sin{\mathrm{A}}\), \(\sin{\mathrm{B}}\)の大小関係は一致するので, \(\mathrm{A}>\mathrm{B}\)がわかる. これから, \(\triangle{\mathrm{ABC}}\)の最大の角は, \(\mathrm{A}\), \(\mathrm{C}\)のいずれかであることがわかる.

① \(\mathrm{A}=120^\circ\)のとき

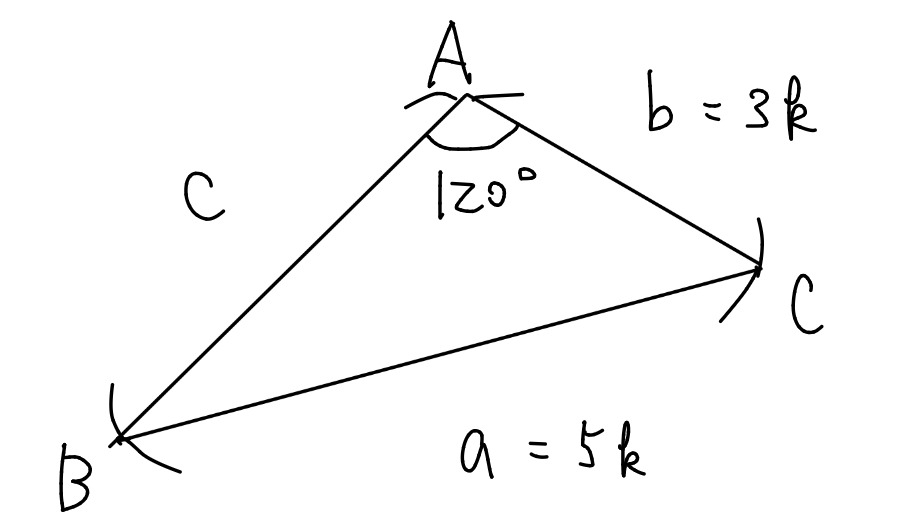
余弦定理から,$$
\begin{align}
&a^2=b^2+c^2-2bc\cos{\mathrm{A}}\\[1.5ex]
&(5k)^2=(3k)^2+c^2-2\cdot 3kc\cdot\left(-\frac{1}{2}\right)\\[1.5ex]
&c^2+3kc-16k^2=0\\[1.5ex]
&c=\frac{-3k\pm\sqrt{9k^2+64k^2}}{2}=\frac{-3\pm\sqrt{73}}{2}k
\end{align}
$$となるが, \(c>0\)より, \(\displaystyle c=\frac{-3+\sqrt{73}}{2}k\)がわかる.

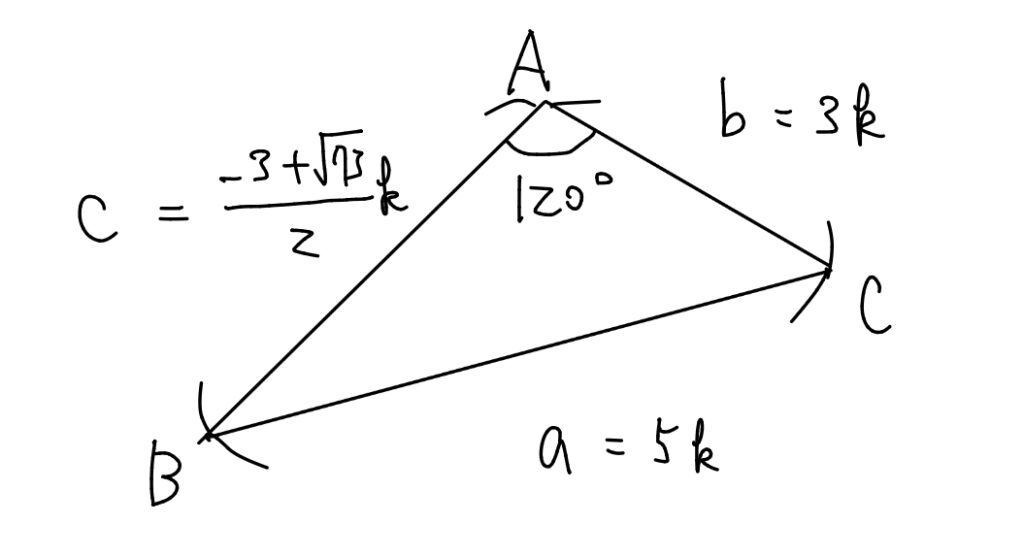
よって余弦定理より,$$
\begin{align}
\cos{\mathrm{B}}&=\frac{c^2+a^2-b^2}{2ca}\\[1.5ex]
&=\frac{\left(\frac{-3+\sqrt{73}}{2}k\right)^2+(5k)^2-(3k)^2}{2\cdot\frac{-3+\sqrt{73}}{2}k\cdot 5k}\\[1.5ex]
&=\frac{9-6\sqrt{73}+73+4\cdot 16}{20(-3+\sqrt{73}}\\[1.5ex]
&=\frac{2\cdot 73-6\sqrt{73}}{20(-3+\sqrt{73})}\\[1.5ex]
&=\frac{2\sqrt{73}(\sqrt{73}-3)}{20(-3+\sqrt{73})}\\[1.5ex]
&=\frac{\sqrt{73}}{10}
\end{align}
$$
$$
\begin{align}
\cos{\mathrm{C}}&=\frac{a^2+b^2-c^2}{2ab}\\[1.5ex]
&=\frac{25k^2+9k^2-\frac{(-3+\sqrt{73})^2}{4}k^2}{2\cdot 5k\cdot 3k}\\[1.5ex]
&=\frac{4\cdot 34-9+6\sqrt{73}-73}{4\cdot 2\cdot 5\cdot 3}\\[1.5ex]
&=\frac{54+6\sqrt{73}}{4\cdot 2\cdot 5\cdot 3}\\[1.5ex]
&=\frac{9+\sqrt{73}}{20}
\end{align}
$$となる. また, \(\mathrm{A}=120^\circ\)より, \(\displaystyle \cos{\mathrm{A}}=-\frac{1}{2}\)である.

② \(\mathrm{C}=120^\circ\)のとき

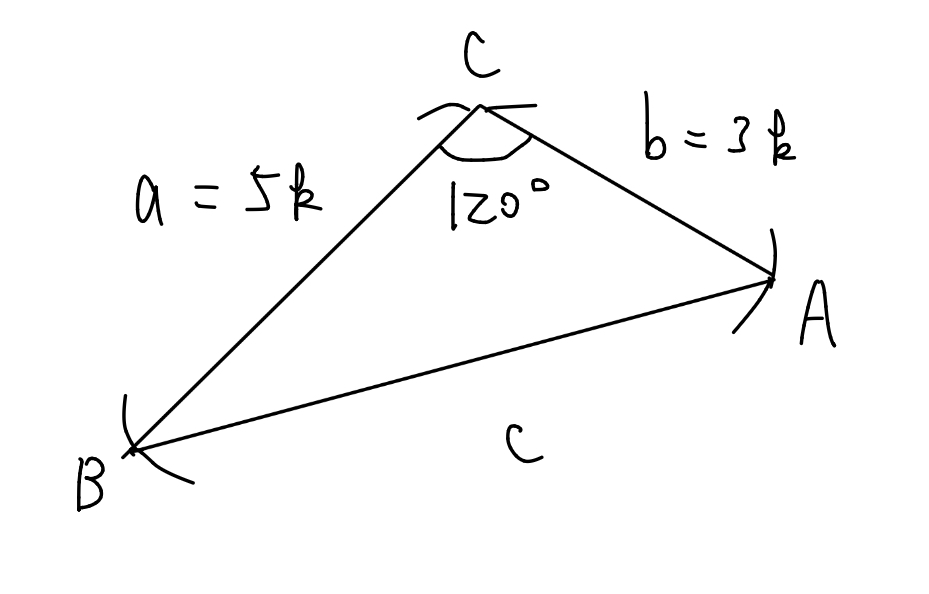
余弦定理から,$$
\begin{align}
c^2&=a^2+b^2-2ab\cos{\mathrm{C}}\\[1.5ex]
&=(5k)^2+(3k)^2-2\cdot 5k \cdot 3k\left(-\frac{1}{2}\right)\\[1.5ex]
&=25k^2+9k^2+15k^2\\[1.5ex]
&=49k^2
\end{align}
$$となり, \(c=7k\)がわかる.

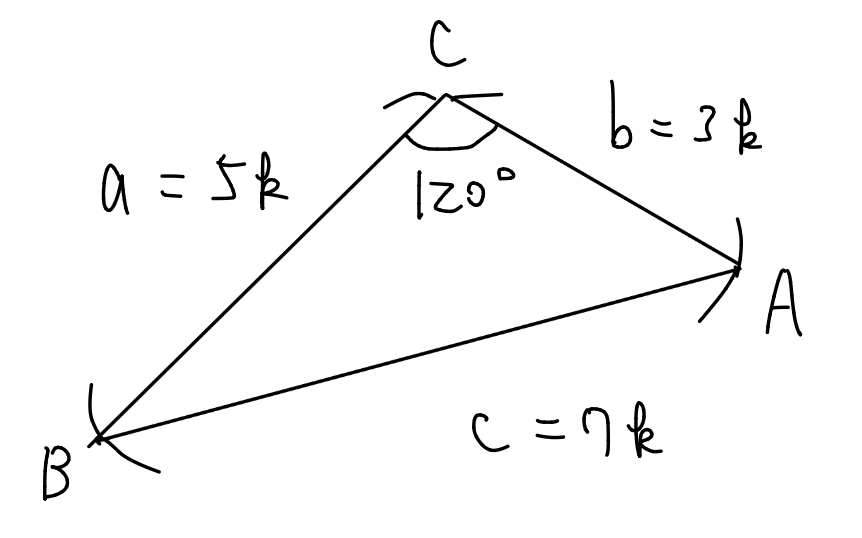
よって余弦定理より,$$
\begin{align}
\cos{\mathrm{A}}&=\frac{b^2+c^2-a^2}{2bc}\\[1.5ex]
&=\frac{9k^2+49k^2-25k^2}{2\cdot 3k \cdot 7k}\\[1.5ex]
&=\frac{33}{2\cdot 3\cdot 7}\\[1.5ex]
&=\frac{11}{14}
\end{align}
$$
$$
\begin{align}
\cos{\mathrm{B}}&=\frac{c^2+a^2-b^2}{2ca}\\[1.5ex]
&=\frac{49k^2+25k^2-9k^2}{2\cdot 7k \cdot 5k}\\[1.5ex]
&=\frac{65}{2\cdot 7\cdot 5}\\[1.5ex]
&=\frac{13}{14}
\end{align}
$$となる. また, \(\mathrm{C}=120^\circ\)より, \(\displaystyle \cos{\mathrm{C}}=-\frac{1}{2}\)である.

以上から, $$
(\cos{\mathrm{A}}, \cos{\mathrm{B}}, \cos{\mathrm{C}})=\left(-\frac{1}{2}, \frac{\sqrt{73}}{10}, \frac{9+\sqrt{73}}{20}\right), \left(\frac{11}{14}, \frac{13}{14}, -\frac{1}{2}\right)
$$となる.