今回はこちらの問題を解いていきます.
\(a\), \(b\)を共に\(1\)以上の実数とし, \(a+b=9\)を満たすとする.
(1) \(\log_3{a}+\log_3{b}\)の最大値, 最小値を求めよ.
(2) \(\log_2{a}+\log_4{b}\)の最大値, 最小値を求めよ.
(2017 一橋大学 [1])
それでは解いていきましょう.
(1) \(a+b=9\)より, \(b=9-a\)であることに注意して,$$
\log_3{a}+\log_3{b}=\log_3{ab}=\log_3{a(9-a)}
$$であり, 対数の底\(3\)は\(1\)より大きいので, 真数\(a(9-1)\)が最大のとき, 対数全体も最大となり, 真数\(a(9-1)\)が最小のとき, 対数全体も最小となる.
真数は\(a\)の\(2\)次関数になっているので平方完成すると,$$
a(9-a)=-a^2+9a=-\left(a-\frac{9}{2}\right)^2+\frac{81}{4}
$$となる.
\(a\geq 1\), \(b=9-a\geq 1\)から, \(1\leq a \leq 8\)であることに注意して, 横軸に\(a\), 縦軸に真数\(a(9-a)\)をとり, グラフを描くと,
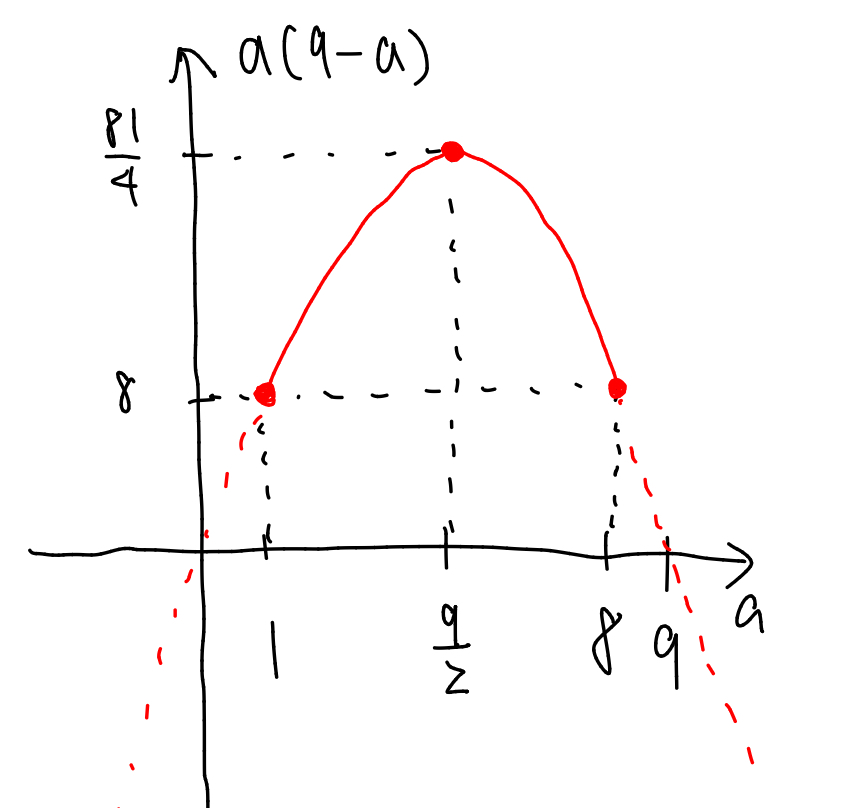
となるので, 真数\(a(9-a)\)は\(\displaystyle a=\frac{9}{2}\)のとき, 最大値\(\displaystyle \frac{81}{4}\), \(a=1, 8\)のとき, 最小値\(8\)をとることがわかる.
よって, \(\log_3{a}+\log_3{b}\)は\(\displaystyle a=b=\frac{9}{2}\)のとき, 最大値\(\displaystyle \log_3{\frac{81}{4}}=4-2\log_3{2}\), \(a=1, b=8\), または \(a=8, b=1\)のとき, 最小値\(\displaystyle \log_3{8}=3\log_3{2}\)をとることがわかる.
(2) まず底を\(2\)に揃えて,$$
\begin{align}
\log_2{a}+\log_4{b}&=\log_2{a}+\frac{\log_2{b}}{\log_2{4}}\\[1.5ex]
&=\log_2{a}+\frac{1}{2}\log_2{b}\\[1.5ex]
&=\frac{1}{2}\left(2\log_2{a}+\log_2{b}\right)\\[1.5ex]
&=\frac{1}{2}\left(\log_2{a^2}+\log_2{b}\right)\\[1.5ex]
&=\frac{1}{2}\log_2{a^2b}\\[1.5ex]
&=\frac{1}{2}\log_2{a^2(9-a)}
\end{align}
$$となり, (1)と同様に対数の底\(2\)は\(1\)より大きいので, 真数が最大のとき, 対数全体も最大に, 真数が最小のとき, 対数全体も最小になる.
真数を\(f(a)=a^2(9-a)\)とおいて, \(1\leq a\leq 8\)の範囲で\(f(a)\)の最大値, 最小値を求める. \(f(a)\)を微分すると,$$
f^\prime(a)=\left(9a^2-a^3\right)^\prime=18a-3a^2=-3a(a-6)
$$となり, \(f^\prime(a)=0\)とおくと, \(a=0, 6\)である. これから増減表を書くと,$$
\begin{array}{|c|c|c|c|c|c|}
\hline
a & 1 & \cdots & 6 & \cdots & 8 \\[1.5ex]
\hline
f^\prime(a) & & + & 0 & – & 0 \\[1.5ex]
\hline
f(a) & 8 & \nearrow & 108 &\searrow& 64 \\[1.5ex]
\hline
\end{array}$$となる. よってこれから, \(f(a)\)は\(a=6\)のとき, 最大値\(108\)を, \(a=1\)のとき, 最小値\(8\)をとることがわかる.
以上から, \(\log_2{a}+\log_4{b}\)は, \(a=6, b=3\)のとき, 最大値\(\displaystyle \frac{1}{2}\log_2{108}=\frac{1}{2}\log_2{2^2\cdot 3^3}=1+\frac{3}{2}\log_2{3}\)を, \(a=1, b=8\)のとき, 最小値\( \displaystyle \log_2{8}=\frac{3}{2}\)をとることがわかる.
youtubeでも解説しています.








