今回はこちらの問題を解いていきます.
\(\displaystyle 0\leq \theta \leq \frac{3\pi}{4}\)のとき, 以下の関数\(f(\theta)=\cos{4\theta}-4\sin^2{\theta}\)の最大値, 最小値を求めよ.
(2004 京都大学 理系 [1])
こちらの問題は3通りの解法を紹介したいと思います.
それでは解いていきましょう.
解法1) \(f(\theta)\)をそのまま微分する解法
\(f(\theta)\)を微分すると,
$$
\begin{align}
f^\prime(\theta)&=-4\sin{4\theta}-8\sin{\theta}\cos{\theta}\\[1.5ex]
&=-8\sin{2\theta}\cos{2\theta}-4\sin{2\theta}\\[1.5ex]
&=-8\sin{2\theta}\left(\cos{2\theta}+\frac{1}{2}\right)
\end{align}
$$となり, \(f^\prime(\theta)=0\)とおくと, \(\sin{2\theta}=0\), または, \(\displaystyle \cos{2\theta}=-\frac{1}{2}\)である.
ここで, \(\displaystyle 0\leq\theta\leq\frac{3\pi}{4}\)より, \(\displaystyle 0\leq 2\theta\leq\frac{3\pi}{2}\)に注意して, \(\sin{2\theta}=0\)から, \(2\theta=0, \pi\)となり, \(\displaystyle \cos{2\theta}=-\frac{1}{2}\)から, \(\displaystyle 2\theta=\frac{2\pi}{3}, \frac{4\pi}{3}\)である.
以上から, \(f^\prime(\theta)=0\)のとき, \(\displaystyle \theta=0, \frac{\pi}{3}, \frac{\pi}{2}, \frac{2\pi}{3}\)である. これから, 増減表を書くと, $$
\begin{array}{|c|c|c|c|c|c|c|c|c|c|}
\hline
\theta & 0 & \cdots & \frac{\pi}{3} & \cdots & \frac{\pi}{2} & \cdots & \frac{2\pi}{3} & \cdots & \frac{3\pi}{4} \\[1.5ex]
\hline
f^\prime(\theta) & 0 & – & 0 & + & 0 & – &0& + & \\[1.5ex]
\hline
f(\theta) & 1 & \searrow & -\frac{7}{2} &\nearrow& -3 &\searrow &-\frac{7}{2}& \nearrow & -3\\[1.5ex]
\hline
\end{array}$$
となり, \(f\(\theta)\)は\(\theta=0\)のとき, 最大値\(1\)を, \(\displaystyle \theta=\frac{\pi}{3}, \frac{2\pi}{3}\)のとき, 最小値\(\displaystyle -\frac{7}{2}\)をとることがわかる.
解法2) \(f(\theta)\)を\cos{\theta}\)で表して, \(4\)次関数の最大最小問題に帰着させる解法
倍角の公式\(\cos{2\theta}=2\cos^2{\theta}-1\)を用いて\(f(\theta)\)を変形すると,$$
\begin{align}
f(\theta)&=(2\cos^2{2\theta}-1)-4(1-\cos^2{\theta})\\[1.5ex]
&=2\left(2\cos^2{\theta}-1\right)^2-1-4+4\cos^2{\theta}\\[1.5ex]
&=2(4\cos^4{\theta}-4\cos^2{\theta}+1)-5+4\cos^2{\theta}\\[1.5ex]
&=8\cos^4{\theta}-4\cos^2{\theta}-3\\[1.5ex]
\end{align}
$$となり, \(f(\theta)\)は\(\cos{\theta}\)の式で表せることがわかる.
\(t=\cos{\theta}\)とおくと, \(\displaystyle 0\leq \theta \leq \frac{3\pi}{4}\)から, \(\displaystyle -\frac{1}{\sqrt{2}}\leq t\leq 1\)であり, $$
f(\theta)=8t^4-4t^2-3
$$と表せる.
\(g(t)=8t^4-4t^2-3\)とおき, \(g(t)\)を微分すると,$$
g^\prime(t)=32t^3-8t=8t(4t^2-1)=8t(2t-1)(2t+1)
$$となるから, \(g^\prime(t)=0\)とおくと, \(\displaystyle t=0, \pm\frac{1}{2}\)となる.
これから増減表を書くと,$$
\begin{array}{|c|c|c|c|c|c|c|c|c|c|}
\hline
t& -\frac{1}{\sqrt{2}} & \cdots & -\frac{1}{2} & \cdots & 0 & \cdots & \frac{1}{2} & \cdots & 1\\[1.5ex]
\hline
g^\prime(t) & & – & 0 & + & 0 & – &0& + & \\[1.5ex]
\hline
g(t) & -3 & \searrow & -\frac{7}{2} &\nearrow& -3 &\searrow &-\frac{7}{2}& \nearrow & 1\\[1.5ex]
\hline
\end{array}$$となり, \(f(\theta)=g(t)\)は\(\displaystyle t=1\), つまり\(\theta=0\)とき, 最大値\(1\)を, \(\displaystyle t=\pm\frac{1}{2}\), つまり\(\displaystyle \theta=\frac{\pi}{3},\frac{2\pi}{3}\)のとき, 最小値\(\displaystyle-\frac{7}{2}\)をとることがわかる.
解法3) \(f(\theta)\)を\(\cos{2\theta}\)で表して, \(2\)次関数の最大最小問題に帰着させる方法
倍角の公式\(\cos{2\theta}=2\cos^2{\theta}-1\), 半角の公式\(\displaystyle \sin^2{\frac{\theta}{2}}=\frac{1-\cos{\theta}}{2}\)を用いて\(f(\theta)\)を変形すると,$$
\begin{align}
f(\theta)&=(2\cos^2{2\theta}-1)-4\cdot\frac{1-\cos{2\theta}}{2}\\[1.5ex]
&=2\cos^2{2\theta}+2\cos{2\theta}-3
\end{align}
$$となり, \(f(\theta)\)は\(\cos{2\theta}\)の式で表せることがわかる.
\(t=\cos{2\theta}\)とおくと, \(\displaystyle 0\leq 2\theta \leq \frac{3\pi}{2}\)から, \(\displaystyle -1 \leq t\leq 1\)であり, $$
f(\theta)=2t^2+2t-3=2\left(t+\frac{1}{2}\right)^2-\frac{7}{2}
$$と表せる.
これから, 横軸に\(t\), 縦軸に\(f(\theta)\)をとってグラフを描くと以下のようになり, \(f(\theta)\)は, \(\displaystyle t=-\frac{1}{2}\)のとき, 最小値\(\displaystyle -\frac{7}{2}\)を, \(\displaystyle t=1\)のとき, 最大値\(1\)をとることがわかる.
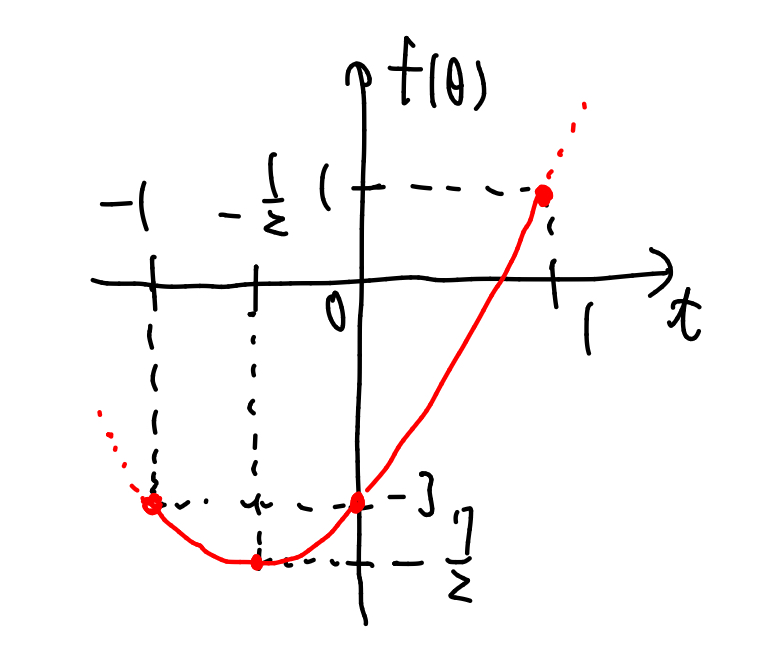
\(\displaystyle 0\leq 2\theta \leq \frac{3\pi}{2}\)の範囲で, \(\displaystyle t=-\frac{1}{2}, -1\)となる, \(\theta\)をそれぞれ求める. \(\displaystyle t=\cos{2\theta}=-\frac{1}{2}\)のときは, \(\displaystyle 2\theta=\frac{2\pi}{3}, \frac{4\pi}{3}\)だから, \(\displaystyle \theta=\frac{\pi}{3}, \frac{2\pi}{3}\)である. また, \(\displaystyle t=\cos{2\theta}=1\)のときは, \(2\theta=0\)より, \(\theta=0\)である.
以上まとめると, \(f(\theta)\)は\(\theta=0\)とき, 最大値\(1\)を, \(\displaystyle \theta=\frac{\pi}{3},\frac{2\pi}{3}\)のとき, 最小値\(\displaystyle-\frac{7}{2}\)をとることがわかる.
youtubeでも解説しています.