今回はこちらの問題を解いていきます.
\(0\leq x < 2\pi\)のとき, 方程式$$
2\sqrt{2}(\sin^3{x}+\cos^3{x})+3\sin{x}\cos{x}=0
$$を満たす\(x\)の個数を求めよ.
(2008 京都大学 文系 [4])
それでは解いていきましょう.
\(t=\sin{x}+\cos{x}\)とおくと,$$
\begin{align}
&t^2=(\sin{x}+\cos{x})^2=\sin^2{x}+2\sin{x}\cos{x}+\cos^2{x}\\[1.5ex]
\iff & \sin{x}\cos{x}=\frac{t^2-1}{2}
\end{align}
$$となる. また, $$
\begin{align}
&t^3=(\sin{x}+\cos{x})^3=\sin^3{x}+3\sin^2{x}\cos{x}+3\sin{x}\cos^2{x}+\cos^3{x}\\[1.5ex]
&t^3=\sin^3{x}+3\sin{x}\cos{x}(\sin{x}+\cos{x})+\cos^3{x}\\[1.5ex]
t&^3=\sin^3{x}+\cos^3{x}+3\cdot\frac{t^2-1}{2}\cdot t\\[1.5ex]
\iff & \sin^3{x}+\cos^3{x}=-\frac{t^3}{2}+\frac{3t}{2}
\end{align}
$$となるから, これを与えられた\(x\)の方程式に代入して,$$
\begin{align}
&2\sqrt{2}\left(-\frac{t^3}{2}+\frac{3t}{2}\right)+3\cdot\frac{t^2-1}{2}=0\\[1.5ex]
\iff & 2\sqrt{2}t^3-3t^2-6\sqrt{2}t+3=0
\end{align}
$$となり, 与えられた方程式を, \(t\)の\(3\)次方程式で表せる.
\(t\)が取り得る値の範囲を求めると, $$
t=\sin{x}+\cos{x}=\sqrt{2}\sin{\left(x+\frac{\pi}{4}\right)}
$$と表すことができ, \(\displaystyle \frac{\pi}{4}\leq x+\frac{\pi}{4}<\frac{9\pi}{4}\)より,$$
-\sqrt{2}\leq t \leq \sqrt{2}
$$とわかる.
\(f(t)\)を\(t\)の\(3\)次方程式の左辺, $$
f(t)=2\sqrt{2}t^3-3t^2-6\sqrt{2}t+3
$$で定義する. \(f(t)\)を微分すると,$$
\begin{align}
f^\prime(t)&=6\sqrt{2}t^2-6t-6\sqrt{2}\\[1.5ex]
&=6(\sqrt{2}t^2-t-\sqrt{2})\\[1.5ex]
&=6(\sqrt{2}t+1)(t-\sqrt{2})
\end{align}
$$となり, \(f^\prime(t)=0\)とすると, \(\displaystyle t=-\frac{1}{\sqrt{2}}\), または, \(t=\sqrt{2}\)である.
これから, \(t\)の取り得る値の範囲\(-\sqrt{2}\leq t\leq \sqrt{2}\)で, \(f(t)\)の増減表を書くと,$$
\begin{array}{|c|c|c|c|c|}
\hline
t & -\sqrt{2} & \cdots & -\frac{1}{\sqrt{2}} & \cdots & \sqrt{2} \\[1.5ex]
\hline
f'(t) & & + & 0 & – & 0 \\[1.5ex]
\hline
f(t) & 1 & \nearrow & \frac{13}{2} &\searrow& -7\\[1.5ex]
\hline
\end{array}$$
となり, 以下のグラフから\(t\)の\(3\)次方程式は, \(-\sqrt{2}\leq t\leq \sqrt{2}\)の範囲で, ただ1つの実数解\(\alpha\)をもつことがわかり, \(\alpha\)は\(0<\alpha<\sqrt{2}\)を満たすこともわかる.
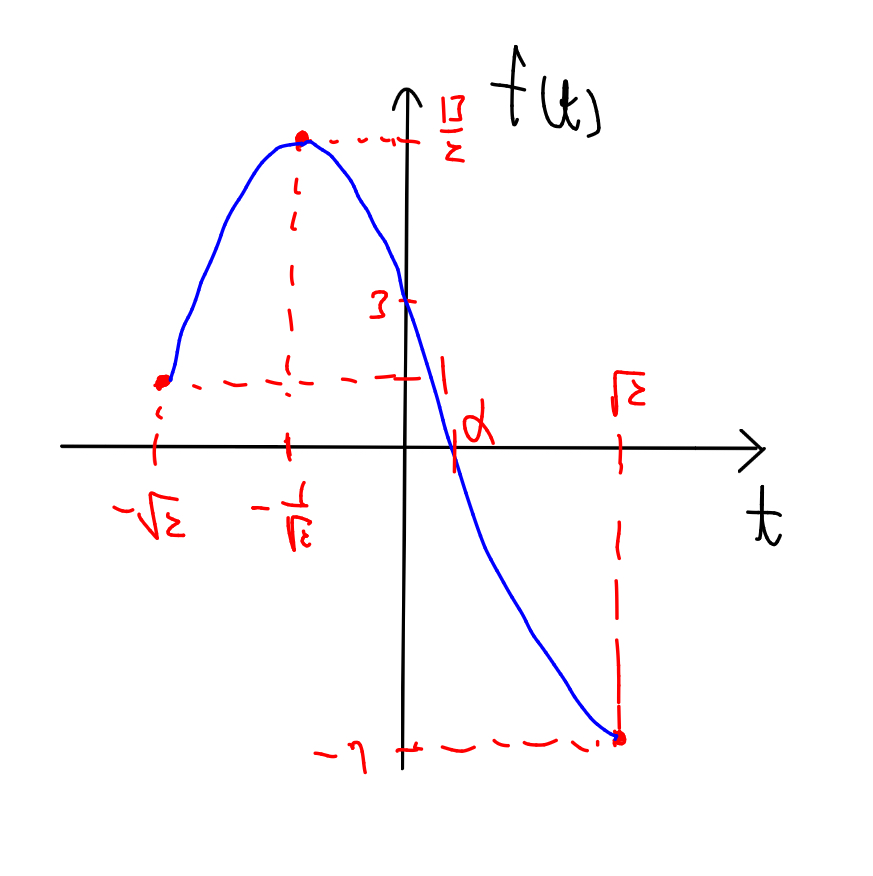
\(t=\sqrt{2}\sin{\left(x+\frac{\pi}{4}\right)}\)のグラフを書くと, \(0<\alpha<\sqrt{2}\)のとき, \(t=\alpha\)となる\(x\)は, \(0\leq x<2\pi\)の範囲に\(2\)つ存在することがわかる.
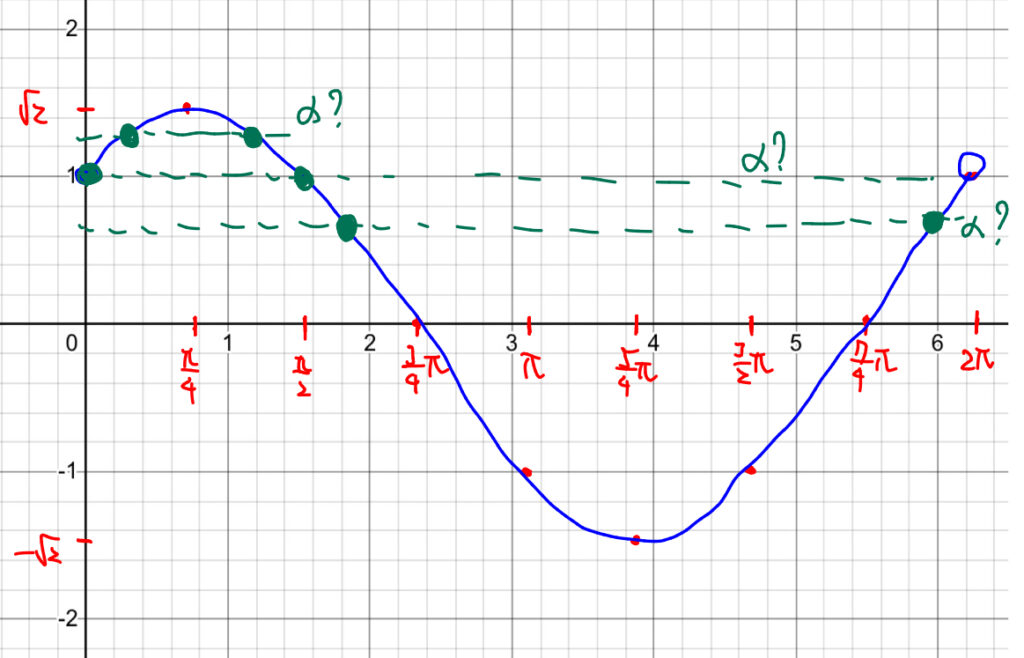
よって, \(0\leq x<2\pi\)の範囲で与えられた方程式を満たす\(x\)の個数は\(2\)であることがわかった.
youtubeでも解説しています.








