【北海道大学入試】部分和の与えられた数列の一般項と逆数和の計算（2021)

(1) 以下, \(\sin\), \(\cos\)の加法定理を用いて式変形を行う. なお, \(\sin{x}\)は順次\(A\)に置き換える.$$
\begin{align}
\sin{5x}&=\sin{(2x+3x)}\\[1.5ex]
&=\sin{2x}\cos{3x}+\cos{2x}\sin{3x}\\[1.5ex]
&=2\sin{x}\cos{x}\cos{(x+2x)}+(1-2\sin^2{x})\sin{(x+2x)}\\[1.5ex]
&=2A\cos{x}(\cos{x}\cos{2x}-\sin{x}\sin{2x})+(1-2A^2)(\sin{x}\cos{2x}+\cos{x}\sin{2x})\\[1.5ex]
&=2A\cos^2{x}(1-2\sin^2{x}-2\sin^2{x})+(1-2A^2)\left\{A(1-2\sin^2{x})+2\sin{x}\cos^2{x}\right\}\\[1.5ex]
&=2A(1-A^2)(1-4A^2)+(1-2A^2)\left\{A(1-2A^2)+2A(1-A^2)\right\}\\[1.5ex]
&=2A(1-5A^2+4A^4)+(1-2A^2)(-4A^3+3A)\\[1.5ex]
&=2A-10A^3+8A^5-4A^3+3A+8A^5-6A^3
&=16A^5-20A^2+5A
\end{align}
$$

(2) (1)で得られた\(\displaystyle \sin{5x}=16A^5-20A^2+5A\)にて, \(\displaystyle x=\frac{\pi}{5}\)として,$$
\sin{\pi}=A(16A^4-20A^2+5)
$$となる. ここで, 左辺は\(0\)であり, \( \displaystyle 0<\frac{\pi}{5}<\frac{\pi}{2}\)より, \(\displaystyle A=\sin{\frac{\pi}{5}}\neq 0\)となるから, 両辺を\(A\)で割ると,$$
16A^4-20A^2+5=0
$$を得る. 求めたいのは\(\displaystyle \sin^2{\frac{\pi}{5}}=A^2\)より, 上の方程式で\(A^2\)を1つの塊として見ることで, これは\(A^2\)に関する2次方程式となっている. よって, $$
A^2=\frac{10\pm \sqrt{(-10)^2-16\cdot 5}}{16}=\frac{5\pm\sqrt{5}}{8}
$$となる.

ここで, \( \displaystyle 0<\frac{\pi}{5}<\frac{\pi}{2}\)より, \(\displaystyle 0<\sin{\frac{\pi}{5}}<\frac{1}{\sqrt{2}}\)なので, \(\displaystyle 0<A^2<\frac{1}{2}\)である. \(\displaystyle \frac{5+\sqrt{5}}{8}>\frac{1}{2}\)より, \(\displaystyle \frac{5+\sqrt{5}}{8}\)は不適である. また, \(\displaystyle 0<\frac{5-\sqrt{5}}{8}<\frac{1}{2}\)も確認できるので, $$
\sin^2{\frac{\pi}{5}}=A^2=\frac{5-\sqrt{5}}{8}
$$である.

(3) 以下の\(\cos\)の定義に用いる単位円の図から, 一般に\(\cos{\theta_1}=\cos{\theta_2}\)となるのは, \(n\)を整数として, \(\theta_2=\theta_1+2n\pi\), もしくは, \(\theta_2=-\theta_1+2n\pi\)と表せるときである.

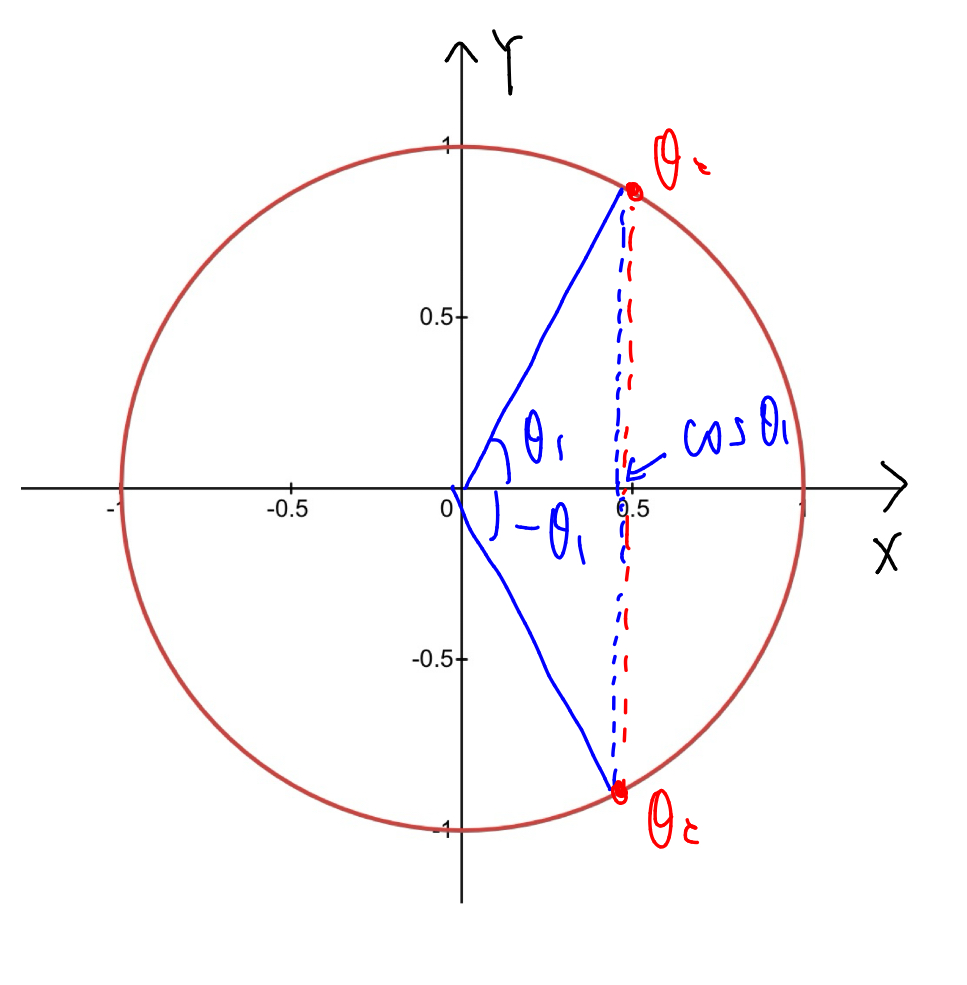
また, この逆も成り立つ. よって, \(\cos{3x}=\cos{7x}\)を満たす\(x\)について, $$
\begin{align}
7x&=3x+2n\pi\\[1.5ex]
7x&=-3x+2n\pi\\[1.5ex]
\end{align}
$$となり, これを整理して, $$
\begin{align}
x&=\frac{n\pi}{2}\\[1.5ex]
x&=\frac{n\pi}{5}\\[1.5ex]
\end{align}
$$のいずれかが成り立つことがわかる.

\(x\geq 0\)に注意して, \(\cos{3x}=\cos{7x}\)となる, \(x\)を小さい方から順に求めると,$$
x_1=0,\,\,x_2=\frac{\pi}{5},\,\,x_3=\frac{2\pi}{5},\,\,x_4=\frac{\pi}{2},\,\,x_5=\frac{3\pi}{5},\,\,x_6=\frac{4\pi}{5}
$$となる. よって, \(x_5\leq x\leq x_6\)のとき, \(\displaystyle\frac{9\pi}{5}\leq 3x\leq \frac{12\pi}{5}\)となり, 以下の図から\(\cos{3x}\)が動く範囲は, \(\displaystyle \cos{\frac{12\pi}{5}}\leq\cos{3x}\leq 1\)となる.

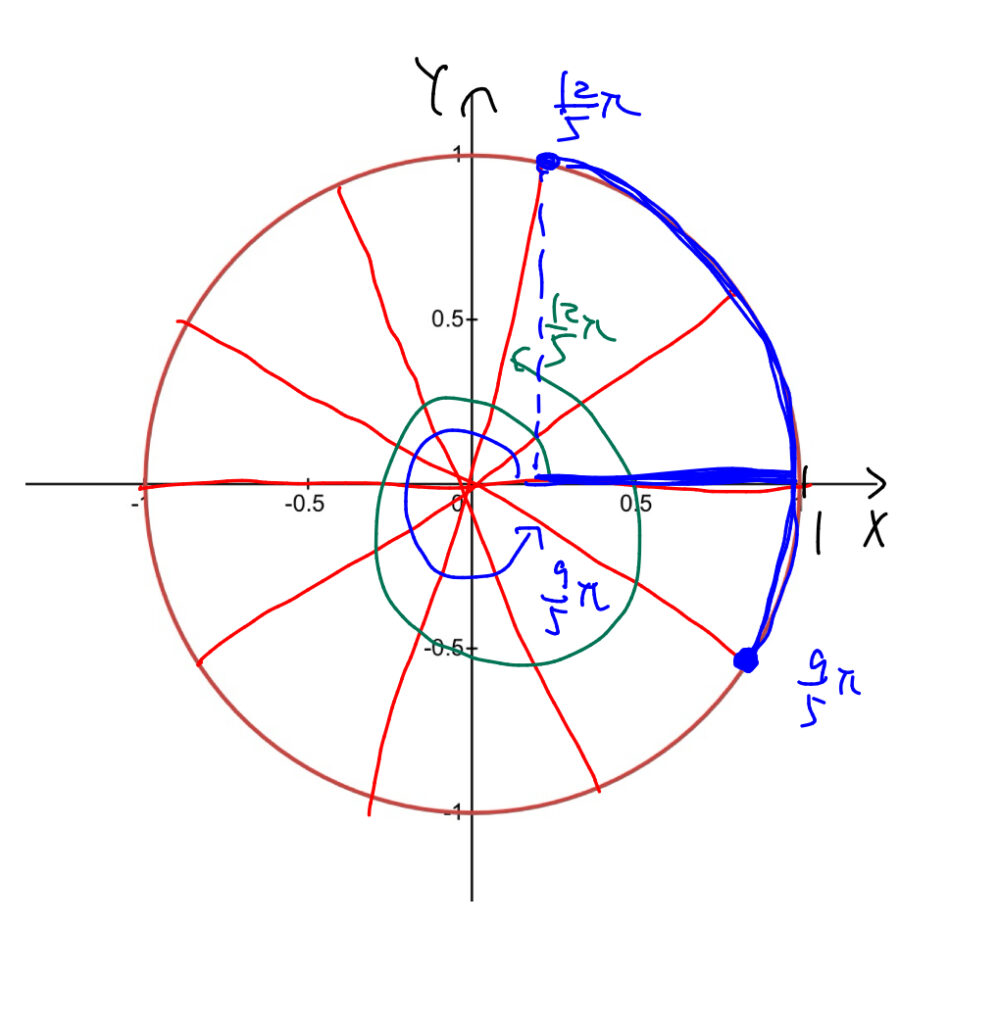
ここで, $$
\cos{\frac{12\pi}{5}}=\cos{\frac{2\pi}{5}}=1-2\sin^2{\frac{\pi}{5}}=\frac{-1+\sqrt{5}}{4}
$$となるから, 求める値域は,$$
\frac{-1+\sqrt{5}}{4}\leq y \leq 1
$$である.