【京都大学入試】絶対値の入った関数のグラフの共通接線と領域の面積(2025)

(1) まず以下の通り関数を定義すると, $$
\begin{align}
f_1(x)&=x^2-2x\\[1.5ex]
f_2(x)&=x^2+2x\\[1.5ex]
g(x)&=x^2-5x+\frac{7}{4}
\end{align}
$$曲線\(C_1\)の方程式は,$$
y=x^2-2|x|=\left\{\begin{array}{ll}f_1(x) & (x\geq 0)\\[1.5ex]
f_2(x)& (x\leq 0)
\end{array}\right.
$$と表せる.

\(t\)を実数とし, 曲線\(\displaystyle C_2:y=g(x)=x^2-5x+\frac{7}{4}\)上の点における接線\(l(t)\)の方程式を求めると, \(g^\prime(x)=2x-5\)より,$$
\begin{align}
y&=g^\prime(t)(x-t)+g(t)\\[1.5ex]
&=(2t-5)(x-t)+t^2-5t+\frac{7}{4}\\[1.5ex]
&=(2t-5)x-t^2+\frac{7}{4}
\end{align}
$$となる. この直線\(l(t)\)が\(y=f_1(x)\), \(y=f_2(x)\)と接するときの\(t\)の値を求める.

① \(y=f_1(x)\)について
先に求めた\(l(t)\)の方程式と, \(y=f_1(x)\)から\(y\)を消去すると,
$$
\begin{align}
&(2t-5)x-t^2+\frac{7}{4}=x^2-2x\\[1.5ex]
\iff & x^2-(2t-3)x+t^2-\frac{7}{4}=0
\end{align}
$$となる. \(l(t)\)が\(y=f_1(x)\)と接するための必要十分条件は, この2次方程式が重解を持つことであるから, 判別式を\(D\)として, $$
\begin{align}
D&=(2t-3)^2-4\left(t^2-\frac{7}{4}\right)=0\\[1.5ex]
\iff &-12t+9+7=0\\[1.5ex]
\iff & t=\frac{4}{3}
\end{align}
$$ となり, \(\displaystyle t=\frac{4}{3}\)のとき, \(l(t)\)は\(y=f_1(x)\)に接する. \(y=f_1(x)\)との接点の\(x\)座標は2次方程式の重解となるので, \(\displaystyle t=\frac{4}{3}\)として, その\(x\)座標は$$
\begin{align}
& x^2-\left(2\cdot\frac{4}{3}-3\right)x+\left(\frac{4}{3}\right)^2-\frac{7}{4}=0\\[1.5ex]
\iff & x^2+\frac{1}{3}+\frac{1}{36}=0\\[1.5ex]
\iff & \left(x+\frac{1}{6}\right)^2=0\\[1.5ex]
\iff & x=-\frac{1}{6}
\end{align}
$$として求まる. しかし, \(\displaystyle -\frac{1}{6}<0\)より, \(y=f_1(x)\)との接点は\(C_1\)に含まれない. よって, \(x\geq 0\)の範囲で\(C_1\)と接するような\(C_2\)との共通接線は存在しない.

② \(y=f_2(x)\)について
先に求めた\(l(t)\)の方程式と, \(y=f_2(x)\)から\(y\)を消去すると,
$$
\begin{align}
&(2t-5)x-t^2+\frac{7}{4}=x^2+2x\\[1.5ex]
\iff & x^2-(2t-7)x+t^2-\frac{7}{4}=0
\end{align}
$$となる. ①と同様に, \(l(t)\)が\(y=f_2(x)\)とも接する\(t\)を求めると, 判別式\(D=0\)から, $$
\begin{align}
D&=(2t-7)^2-4\left(t^2-\frac{7}{4}\right)=0\\[1.5ex]
\iff &-28t+49+7=0\\[1.5ex]
\iff & t=2
\end{align}
$$ となる. \(y=f_2(x)\)との接点の\(x\)座標は2次方程式の重解となるので, \(t=2\)として, その\(x\)座標は$$
\begin{align}
& x^2-\left(2\cdot 2-7\right)x+2^2-\frac{7}{4}=0\\[1.5ex]
\iff & x^2+3x+\frac{9}{4}=0\\[1.5ex]
\iff & \left(x+\frac{3}{2}\right)^2=0\\[1.5ex]
\iff & x=-\frac{3}{2}
\end{align}
$$として求まり, \(\displaystyle -\frac{3}{2}<0\)より, \(y=f_2(x)\)との接点は\(C_1\)に含まれる. よって, これが唯一の\(C_1\), \(C_2\)の共通接線となり, これが\(l_2\)である. \(t=2\)から\(l_2\)の方程式は,
$$
y=(2\cdot 2-5)x-2^2+\frac{7}{4}=-x-\frac{9}{4}
$$となる.

(2) 各曲線, 直線のグラフと, 面積を求める図形を描くと以下のようになる.

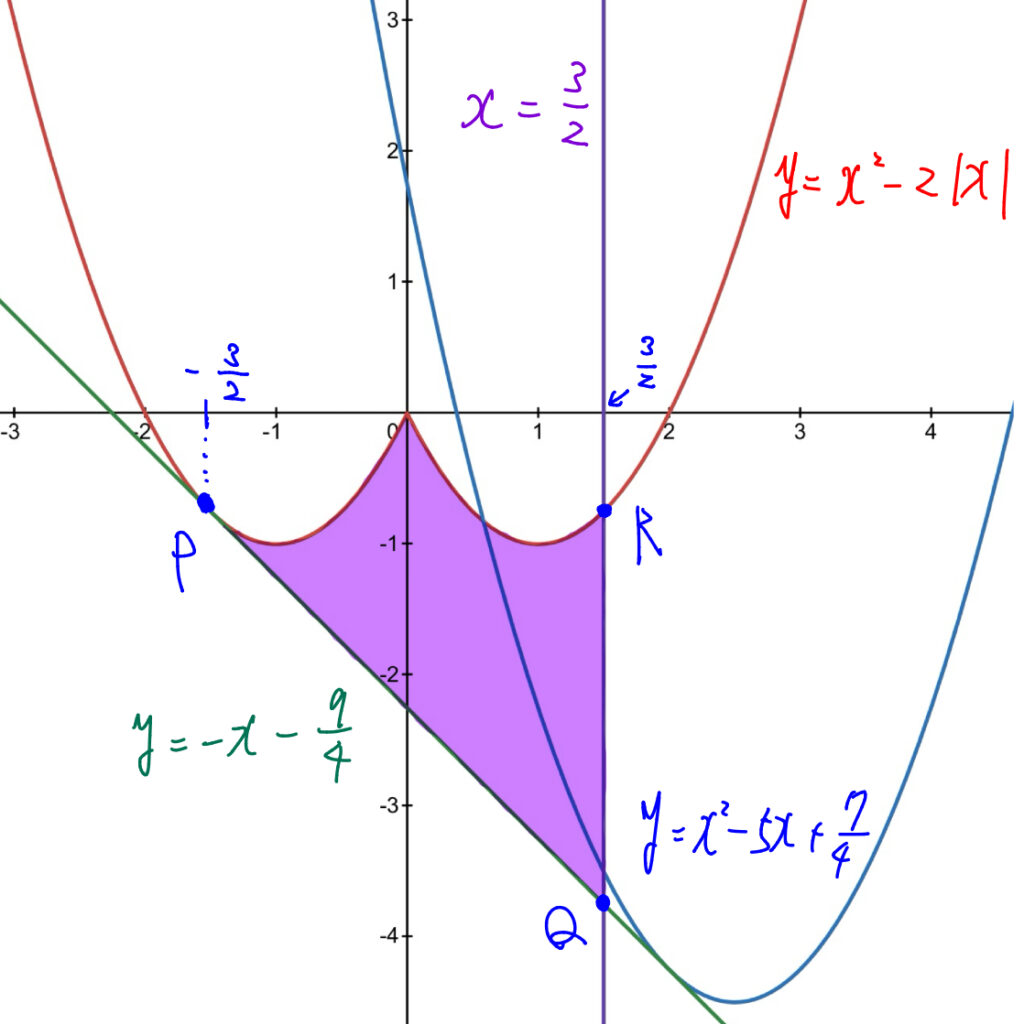
(1)から, \(\displaystyle \alpha=-\frac{3}{2}\)であり, 図形の面積\(S\)は以下のように求まる.
$$
\begin{align}
S&=\int_{-\frac{3}{2}}^0\left\{x^2+2x-\left(-x-\frac{9}{4}\right)\right\}\,dx\\[1.5ex]
&\qquad +\int_0^{\frac{3}{2}}\left\{x^2-2x-\left(-x-\frac{9}{4}\right)\right\}\,dx\\[1.5ex]
&=\int_{-\frac{3}{2}}^0\left(x^2+3x+\frac{9}{4}\right)\,dx\\[1.5ex]
&\qquad + \int_0^{\frac{3}{2}}\left(x^2-x+\frac{9}{4}\right)\,dx\\[1.5ex]
&=\left[\frac{x^3}{3}+\frac{3}{2}x^2+\frac{9}{4}x\right]_{-\frac{3}{2}}^0\\[1.5ex]
&\qquad +\left[\frac{x^3}{3}-\frac{1}{2}x^2+\frac{9}{4}x\right]_0^{\frac{3}{2}}\\[1.5ex]
&=-\left\{\frac{1}{3}\left(-\frac{3}{2}\right)^3+\frac{3}{2}\left(-\frac{3}{2}\right)^2+\frac{9}{4}\cdot\left(-\frac{3}{2}\right)\right\}\\[1.5ex]
&\qquad +\left\{\frac{1}{3}\left(\frac{3}{2}\right)^3-\frac{1}{2}\left(\frac{3}{2}\right)^2+\frac{9}{4}\cdot\left(\frac{3}{2}\right)\right\}\\[1.5ex]
&=-\left(-\frac{9}{8}+\frac{27}{8}-\frac{27}{8}\right)\\[1.5ex]
&\qquad +\left(\frac{9}{8}-\frac{9}{8}+\frac{27}{8}\right)\\[1.5ex]
&=\frac{9}{8}+\frac{27}{8}=\frac{36}{8}=\frac{9}{2}
\end{align}
$$となり, 面積が求まった.