今回はこちらの問題を解いていきます.
実数\(a, b\)に対して, 以下の\(\theta\)についての方程式が, 実数解をもつような\((a,b)\)の存在範囲を座標平面上に図示せよ.$$
\cos{2\theta}=a\sin{\theta}+b
$$
(2023 大阪大学 文系 [1])
それでは解いていきましょう.
与えられた\(\theta\)に関する方程式\(\displaystyle \cos{2\theta}=a\sin{\theta}+b\)を①とおく.
\(\cos{2\theta}=1-2\sin^2{\theta}\)より, 与えられた方程式は,
$$
2\sin^2{\theta}+a\sin{\theta}+b-1=0
$$と変形できる. ここで, \(t=\sin{\theta}\)とおくと, この方程式は,
$$
2t^2+at+b-1=0\,\,\,・・・②
$$と変形でき, これは\(t\)に関する2次方程式となる. \(-1\leq t\leq 1\)なる\(t\)に対し, \(\sin{\theta}=t\)となる\(\theta\)が存在し, \(|t|>1\)なる\(t\)に関しては\(\sin{\theta}=t\)となる\(\theta\)が存在しないことに注意すると, この\(t\)に関する方程式が\(-1\leq t\leq 1\)の範囲の解を持つことが, ①が実数解を持つ必要十分条件となることがわかる.
\(f(t)=2t^2+at+b-1\)とおくと, $$
f(t)=2\left(t+\frac{a}{4}\right)^2-\frac{a^2}{8}+b-1
$$と変形できるので, 横軸に\(t\), 縦軸に\(y\)をとると, \(y=f(t)\)のグラフは, \(\displaystyle \left(-\frac{a}{4}, -\frac{a^2}{8}+b-1\right)\)を頂点とする, 下に凸の放物線となる. この放物線の軸は\(\displaystyle t=-\frac{a}{4}\)であり, 軸に関して場合分けをすることで, ②が\(-1\leq t\leq 1\)の範囲に解を持つ, 言い換えると, \(y=f(t)\)が\(t\)軸と\(-1\leq t\leq 1\)の範囲で共有点を持つ\((a,b\))の条件を調べていく.
1) 軸が直線\(t=-1\)より左にあるとき, つまり, \( \displaystyle -\frac{a}{4}<-1 \iff a>4\)のとき
このときグラフは以下の図のようになる.
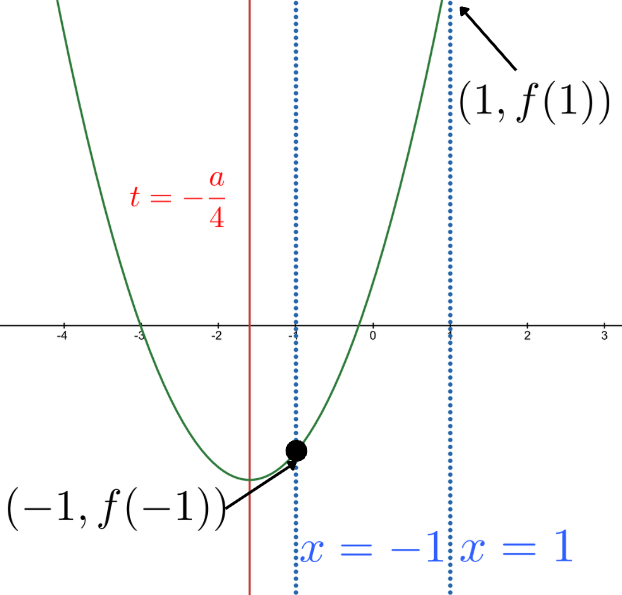
よって, \(y=f(t)\)が\(t\)軸と\(-1\leq t\leq 1\)で共有点を持つ必要十分条件は,
$$
f(-1)\leq 0 \,\,\,かつ\,\,\,f(1)\geq 0
$$となる.$$
\begin{align}
&f(-1)=2-a+b-1=-a+b+1\leq 0\\[1.5ex]
\iff & b\leq a-1
\end{align}
$$であり, $$
\begin{align}
&f(1)=2+a+b-1=a+b+1\geq 0\\[1.5ex]
\iff & b\geq -a-1
\end{align}
$$となる.
2) 軸が\(-1\leq t\leq 1\)の領域にあるとき, つまり, \(\displaystyle -1\leq -\frac{a}{4}\leq 1 \iff -4\leq t\leq 4\)のとき
このときグラフは以下の図のようになる.
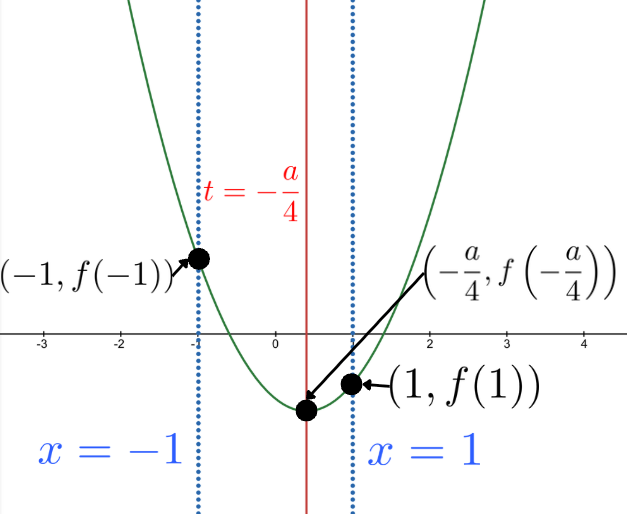
よって, \(y=f(t)\)が\(t\)軸と\(-1\leq t\leq 1\)で共有点を持つ必要十分条件は, $$
f\left(-\frac{a}{4}\right)\leq 0\,\,\,かつ\,\,\,「f(-1)\geq 0\,\,\,または\,\,\,f(1)\geq 0」
$$となる. \(\displaystyle f\left(-\frac{a}{4}\right)\leq 0\), \(f(-1)\geq 0\), \(f(1)\geq 0\)をそれぞれ変形すると.
$$
\begin{align}
&f\left(-\frac{a}{4}\right) = -\frac{a^2}{8}+b-1 \leq 0\\[1.5ex]
\iff & b\leq \frac{a^2}{8}+1
\end{align}
$$
$$
\begin{align}
&f(-1)=2-a+b-1=-a+b+1\geq 0\\[1.5ex]
\iff & b\geq a-1
\end{align}
$$
$$
\begin{align}
&f(1)=2+a+b-1=a+b+1\geq 0\\[1.5ex]
\iff & b\geq -a-1
\end{align}
$$である.
③ 軸が直線\(t=1\)より右にあるとき, つまり, \( \displaystyle -\frac{a}{4}>1 \iff a<-4\)のとき
このときグラフは以下の図のようになる.
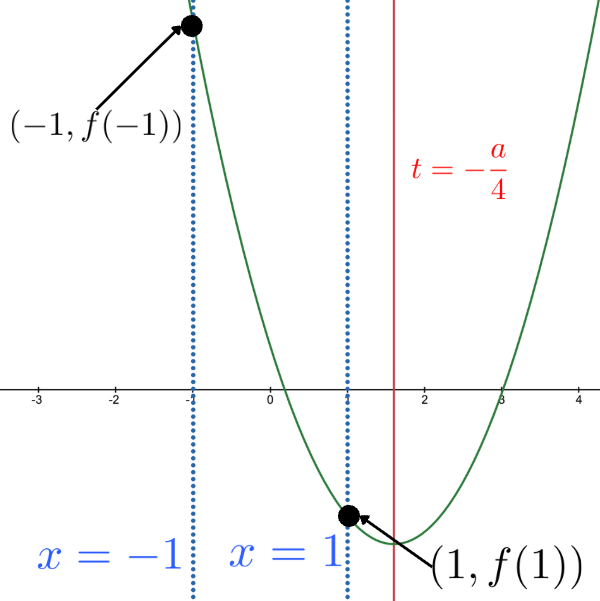
よって, \(y=f(t)\)が\(t\)軸と\(-1\leq t\leq 1\)で共有点を持つ必要十分条件は,
$$
f(-1)\geq 0 \,\,\,かつ\,\,\,f(1)\leq 0
$$となる.$$
\begin{align}
&f(-1)=2-a+b-1=-a+b+1\geq 0\\[1.5ex]
\iff b & \geq a-1
\end{align}
$$であり, $$
\begin{align}
&f(1)=2+a+b-1=a+b+1\leq 0\\[1.5ex]
\iff & b\leq -a-1
\end{align}
$$となる.
1), 2), 3)より, \(y=f(t)\)が\(t\)軸と\(-1\leq t\leq 1\)で共有点を持つ\((a,b)\)の領域を図示すると, 以下のようになる.
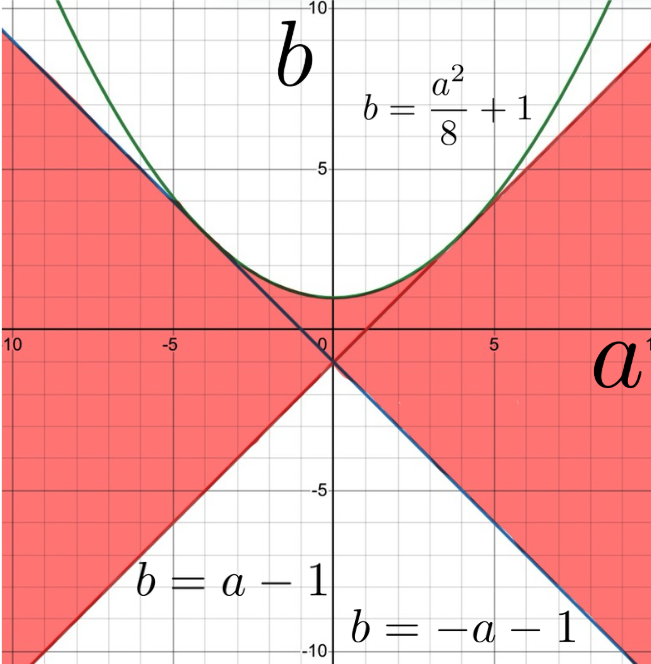
これが, ①が実数解を持つ領域そのものである.
youtubeでも解説しています.








