今回はこちらの問題を解いていきます.
実数\(a\)が\(-2\leq a <2 \)の範囲を動くとき, 次の連立不等式の表す領域の面積\(S(a)\)の最大値を求めよ.
$$
\left\{
\begin{aligned}
& y\leq -\frac{1}{2}x^2+2 \\[1.5ex]
& y\geq |x^2+a| \\[1.5ex]
& -1\leq x \leq 1
\end{aligned}
\right.
$$(2025 東京大学 文系 [4])
こちらはなかなかの難問です. 最初は時間をかけても良いので, 丁寧にグラフを書いて考えてみてください.
それでは解いていきましょう.
連立不等式の表す領域は, \(a\)の値の範囲によって以下の4パターンに分けられる.
① \(-2\leq a \leq -1\)のとき
領域は以下の通りで, \(y=|x^2+a|\)は\((0,-a)\)で\(y\)軸と交わり, \(a\)を大きくしていくと領域が単調に拡大し, \(S(a)\)が\(a\)に関して単調増加であることがわかる.
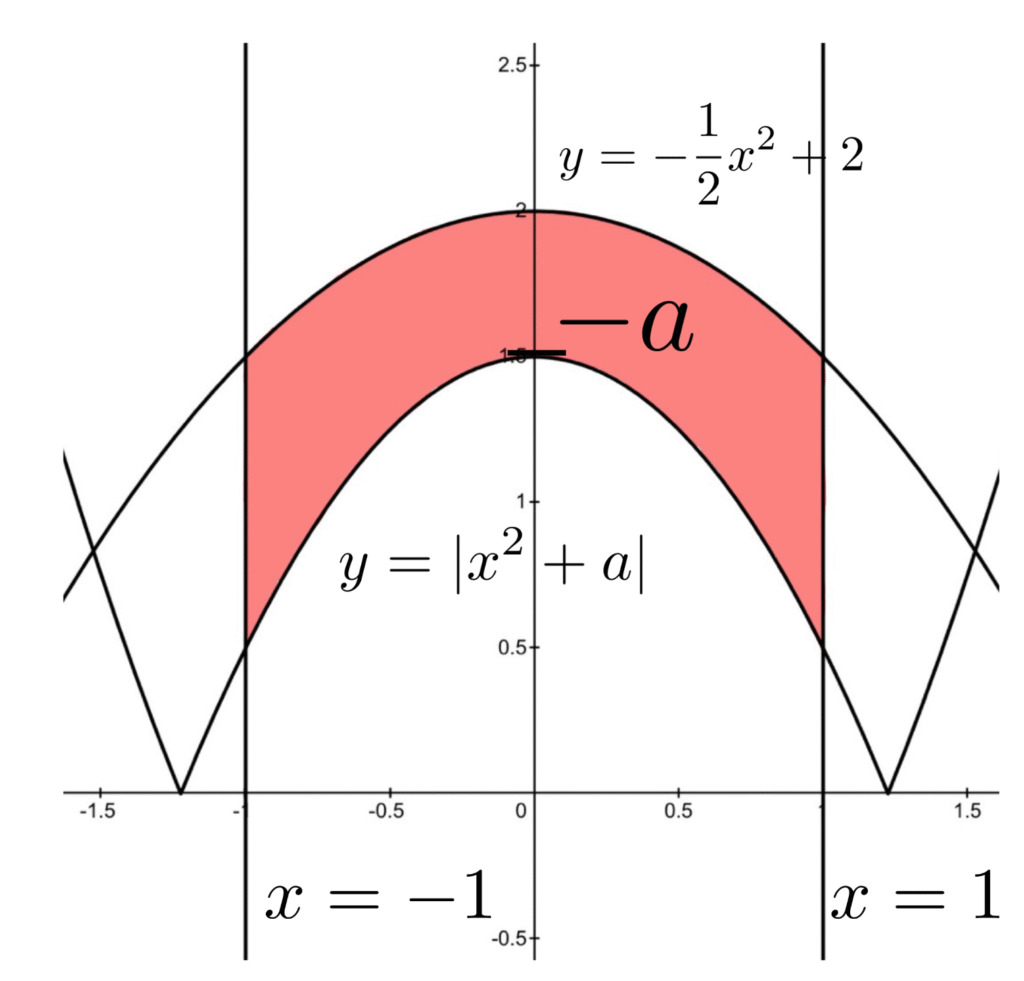
② \(-1\leq a\leq 0\)のとき
領域は以下の通り.
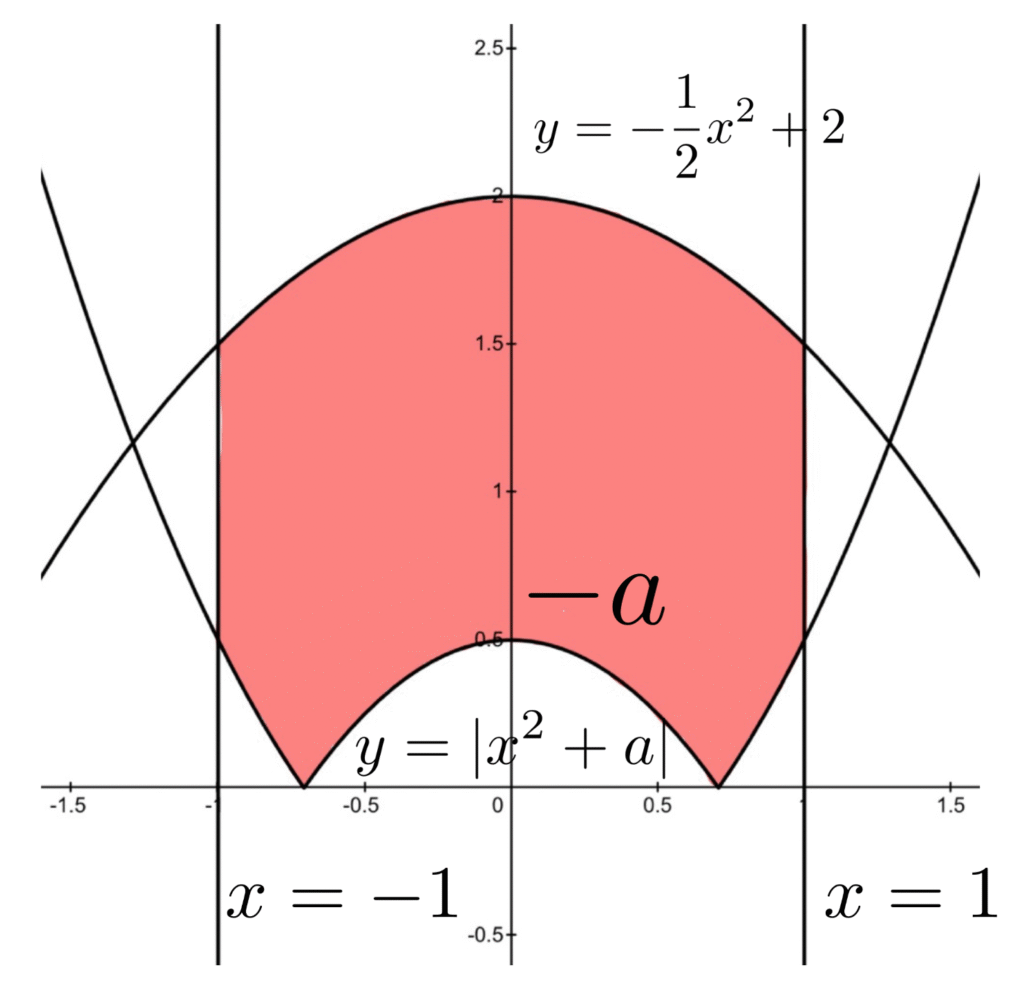
③ \(\displaystyle 0\leq a \leq \frac{1}{2}\)のとき
領域は以下の通りで, \(y=|x^2+a|\)は\((0,a)\)で\(y\)軸と交わり, \(a\)を大きくしていくと領域が単調に縮小し, \(S(a)\)が\(a\)に関して単調減少であることがわかる.
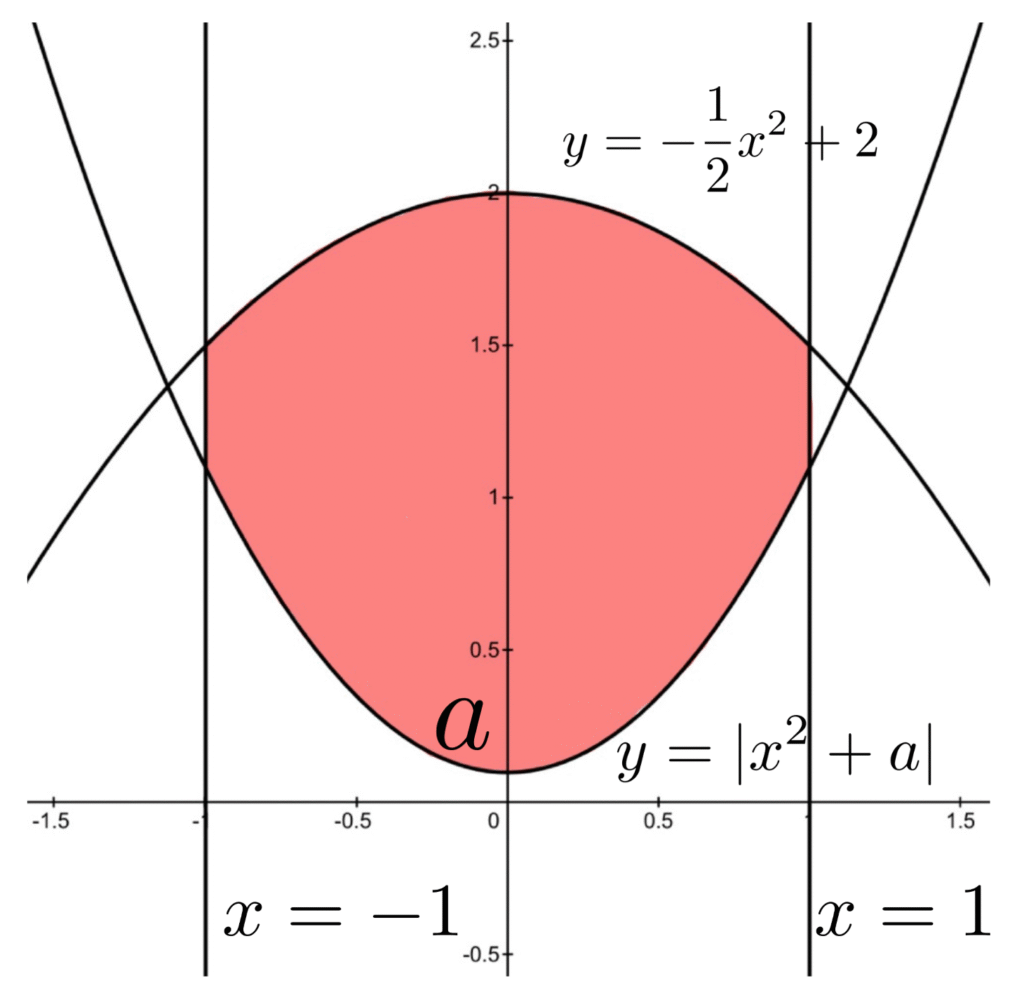
④ \(\displaystyle \frac{1}{2} \leq a <2\)のとき
領域は以下の通りで, \(y=|x^2+a|\)は\((0,a)\)で\(y\)軸と交わり, \(a\)を大きくしていくと領域が単調に縮小し, \(S(a)\)が\(a\)に関して単調減少であることがわかる.
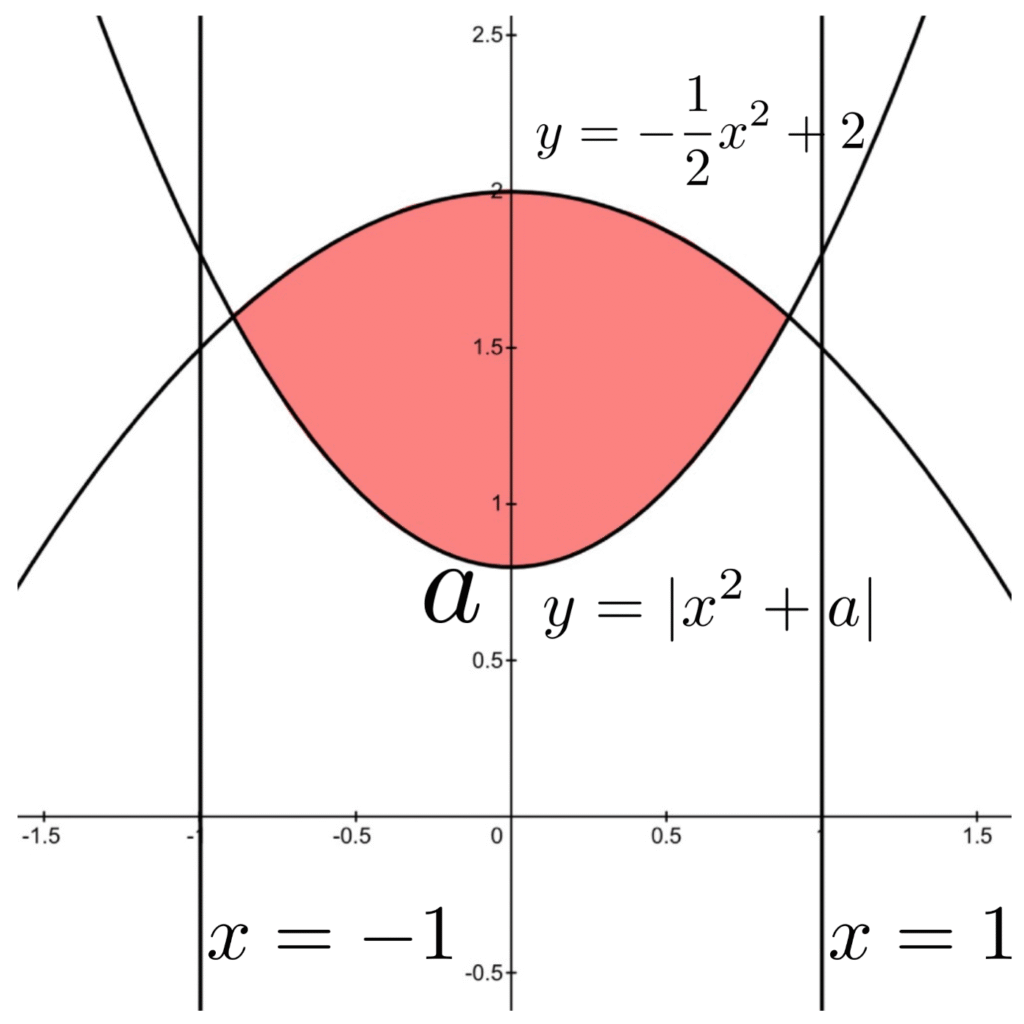
①〜④より, \(S(a)\)が最大値をとる\(a\)は②の\(-1\leq a \leq 0\)の範囲にあることがわかる. よって, 以下では, ②の\(-1\leq a \leq 0\)で\(S(a)\)を計算していく.
$$
S(a)=\int_{-1}^1\left\{-\frac{1}{2}x^2+2-|x^2+a|\right\}\,dx
$$であるが, 被積分関数は\(x\)に関して偶関数であり, また, \(y=|x^2+a|\)と\(x\)軸との共有点は\((-\sqrt{-a},0)\), \((\sqrt{-a},0)\)であることに注意して, \(S(a)\)は以下のように変形できる.
$$
\begin{align}
S(a)&=2\int_0^1\left\{-\frac{1}{2}x^2+2-|x^2+a|\right\}\,dx\\[1.5ex]
&=2\int_0^\sqrt{-a}\left\{-\frac{1}{2}x^2+2-|x^2+a|\right\}\,dx+2\int_\sqrt{-1}^1\left\{-\frac{1}{2}x^2+2-|x^2+a|\right\}\,dx
\end{align}
$$ 式中の2つの積分を計算していく.
まず, 1つ目の積分は, \(0\leq x \leq \sqrt{-a}\)で\(x^2+a\leq 0\)より,$$
\begin{align}
\int_0^\sqrt{-a}\left\{-\frac{1}{2}x^2+2-|x^2+a|\right\}\,dx&=\int_0^\sqrt{-a}\left\{-\frac{1}{2}x^2+2+(x^2+a)\right\}\,dx\\[1.5ex]
&=\int_0^\sqrt{-a}\left\{\frac{1}{2}x^2+2+a\right\}\,dx\\[1.5ex]
&=\left[\frac{x^3}{6}+(2+a)x\right]_0^{\sqrt{-a}}\\[1.5ex]
&=-\frac{a\sqrt{-a}}{6}+(2+a)\sqrt{-a}\\[1.5ex]
&=\frac{5a\sqrt{-a}}{6}+2\sqrt{-a}
\end{align}
$$となる.
次に, 2つ目の積分は, \(\sqrt{-a}\leq x \leq 1\)で\(x^2+a\geq 0\)より,$$
\begin{align}
\int_\sqrt{-a}^2\left\{-\frac{1}{2}x^2+2-|x^2+a|\right\}\,dx&=\int_\sqrt{-a}^2\left\{-\frac{1}{2}x^2+2-(x^2+a)\right\}\,dx\\[1.5ex]
&=\int_\sqrt{-a}^1\left\{-\frac{3}{2}x^2+2-a\right\}\,dx\\[1.5ex]
&=\left[-\frac{x^3}{2}+(2-a)x\right]_{\sqrt{-a}}^1\\[1.5ex]
&=-\frac{1}{2}+2-a-\frac{a\sqrt{-a}}{2}-(2-a)\sqrt{-a}\\[1.5ex]
&=\frac{3}{2}-a+\frac{a\sqrt{-a}}{2}-2\sqrt{-a}
\end{align}
$$となる.
よってこれらを\(S(a)\)に代入して,
$$
\begin{align}
S(a)&=2\left(\frac{5a\sqrt{-a}}{6}+2\sqrt{-a}\right)+2\left(\frac{3}{2}-a+\frac{a\sqrt{-a}}{2}-2\sqrt{-a}\right)\\[1.5ex]
&=\frac{8}{3}a\sqrt{-a}-2a+3
\end{align}
$$となる.
最後に, \(-a\leq a \leq 0\)の範囲で\(\displaystyle S(a)=\frac{8}{3}a\sqrt{-a}-2a+3\)の最大値を求める. \(\displaystyle t=\sqrt{-a}\)とおくと, \(t\)が取り得る値の範囲は\(0\leq t\leq 1\)となる. \(a=-t^2\)であるから, \(S(a)\)は,
$$
S(a)=-\frac{8}{3}t^3+2t^2+3
$$と\(t\)の関数で表すことができる. この右辺を\(\displaystyle f(t)=-\frac{8}{3}t^3+2t^2+3\)とおき, \(0\leq t\leq 1\)の範囲で最大値を求める.
$$
f^\prime(t)=-8t^2+4t=-8t\left(t-\frac{1}{2}\right)
$$より, \(f^\prime(t)=0\)とすると, \(\displaystyle t=0, \frac{1}{2}\)である. これから増減表を書くと以下となり,
$$
\begin{array}{|c|c|c|c|c|}
\hline
t & 0 & \cdots & \frac{1}{2} & \cdots & 1\\[1.5ex]
\hline
f'(t) & 0 & + & 0 & – & – \\[1.5ex]
\hline
f(t) & & \nearrow & & \searrow & \\[1.5ex]
\hline
\end{array}
$$\(f(t)\)は\(\displaystyle t=\frac{1}{2}\)のとき最大値をとることがわかる. 最大値は,
$$
f\left(\frac{1}{2}\right)=-\frac{8}{3}\left(\frac{1}{2}\right)^2+2\cdot\left(\frac{1}{2}\right)^2+3=\frac{19}{6}
$$となる. \(\displaystyle t=\frac{1}{2}\)のとき, \(a=-\frac{1}{4}\)であることから, \(S(a)\)は\(\displaystyle a=-\frac{1}{4}\)のとき, 最大値\(\displaystyle \frac{19}{6}\)をとることがわかる.
こちらの問題はなかなかの難問だと思います. ①から④の場合分けを正確に行うだけでもかなり神経を使わないといけないですし, その先で\(S(a)\)が最大となるのは②のパターンだけを確認すればよいと判断するのは, 本番の入試会場ではとても難しいのではないかと思います. 最初の関門を抜ければその後は計算だけなので比較的容易ではあるのですが, 全体を通して計算量も多いので, グラフを書く力, グラフから考察する力, 計算力など, 多くの能力が試される良問かつ難問だと思います.
youtubeでも解説しています.








