【京都大学入試】恒等式を満たすような2次式が存在する条件(2025)

2次式\(f(x)\)は実数\(p\neq 0\), \(q\), \(r\)を用いて
$$
f(x)=px^2+qx+r
$$と表すことができる. この\(f(x)\)に対して, \(f(f(x))+c\)を計算すると,
$$
\begin{align}
f(f(x))+c&=p(px^2+qx+r)^2+q(px^2+qx+r)+r + c\\[1.5ex]
&=p\left(p^2x^4+2pqx^3+\left(2pr+q^2\right)x^2+2qrx+r^2\right)\\[1.5ex]
&\qquad +pqx^2+q^2x+qr+r+c\\[1.5ex]
&=p^3x^4+2p^2qx^3+p\left(2pr+q^2+q\right)x^2+(2pqr+q^2)x\\[1.5ex]
&\qquad +pr^2+qr+r+c
\end{align}
$$となる.

これが, \(\displaystyle \frac{1}{8}x^4+ax^3+bx^2\)と一致するような\(p\), \(q\), \(r\), \(c\)が存在する\(a\), \(b\)の条件を考えていく. まず最高次\(x^4\)の係数を比べて,
$$
\frac{1}{8}=p^3
$$より, $$
p=\frac{1}{2}
$$となり, これを\(f(f(x))+c\)の式に代入すると,
$$
\begin{align}
f(f(x))+c&=\frac{1}{8}x^4+\frac{q}{2}x^3+\frac{1}{2}\left(r+q^2+q\right)x^2+q(q+r)x\\[1.5ex]
&\qquad +\frac{r^2}{2}+qr+c
\end{align}
$$となる.

これから各係数を比べて,
$$
\begin{align}
a&=\frac{q}{2}\,\,\,・・・①\\
b&=\frac{1}{2}\left(r+q^2+q\right)\,\,\,・・・②\\
0&=q(q+r)\,\,\,・・・③\\
0&=\frac{r^2}{2}+qr+r+c\,\,\,・・・④
\end{align}
$$となる. \(c\)は④以外には現れないから, ①, ②, ③を満たす\(q\), \(r\)に対して,
$$
c=-\frac{r^2}{2}-qr-r
$$とおけば, ④は常に成り立つようにできる. ③は, \(q=0\) または, \(r=-q\)であれば成り立つので, 各場合において①, ②が成り立つ\(q\), \(r\)が存在する\(a\), \(b\)の条件を見ていく.

1) \(q=0\)のとき
①より\(a=0\)となる必要がある. また, ②より\(\displaystyle b=\frac{r}{2}\)であるから, \(b\)に対して, \(r=2b\)ととれば②は満たされる. よって\(a=0\)であれば, \(b\)の値に依らず与えられた条件を満たす2次式\(f(x)\)と, 実数\(c\)が存在することがわかる. 具体的には,
$$
\begin{align}
f(x)&=\frac{1}{2}x^2+2b,\,\,\,\left(p=\frac{1}{2}, q=0, r=2b\right)\\[1.5ex]
c&=-\frac{r^2}{2}-qr-r=-2b^2-2b
\end{align}
$$ととればよい.

2) \(r=-q\)のとき
①は, \(a\)に対して\(q=2a\)とすれば満たされる. ②は, \(\displaystyle b=\frac{q^2}{2}\)となり, \(q=2a\)とする必要があることから, \(\displaystyle b=2a^2\)となる. つまり, 任意の\(a\)に対して\(b=2a^2\)であれば, 与えられた条件を満たす2次式\(f(x)\)と, 実数\(c\)が存在することがわかる. 具体的には,
$$
\begin{align}
f(x)&=\frac{1}{2}x^2+2ax-2a,\,\,\,\left(p=\frac{1}{2}, q=2a, r=-2a\right)\\[1.5ex]
c&=-\frac{r^2}{2}-qr-r=-2a^2+4a^2+2a\\[1.5ex]
&=2a^2+2a\,(=2a+b)
\end{align}
$$ととればよい. 逆に\(b\neq 2a^2\)であれば, ①, ②を同時に満たす, \(q\), \(r=-q\)は存在しない.

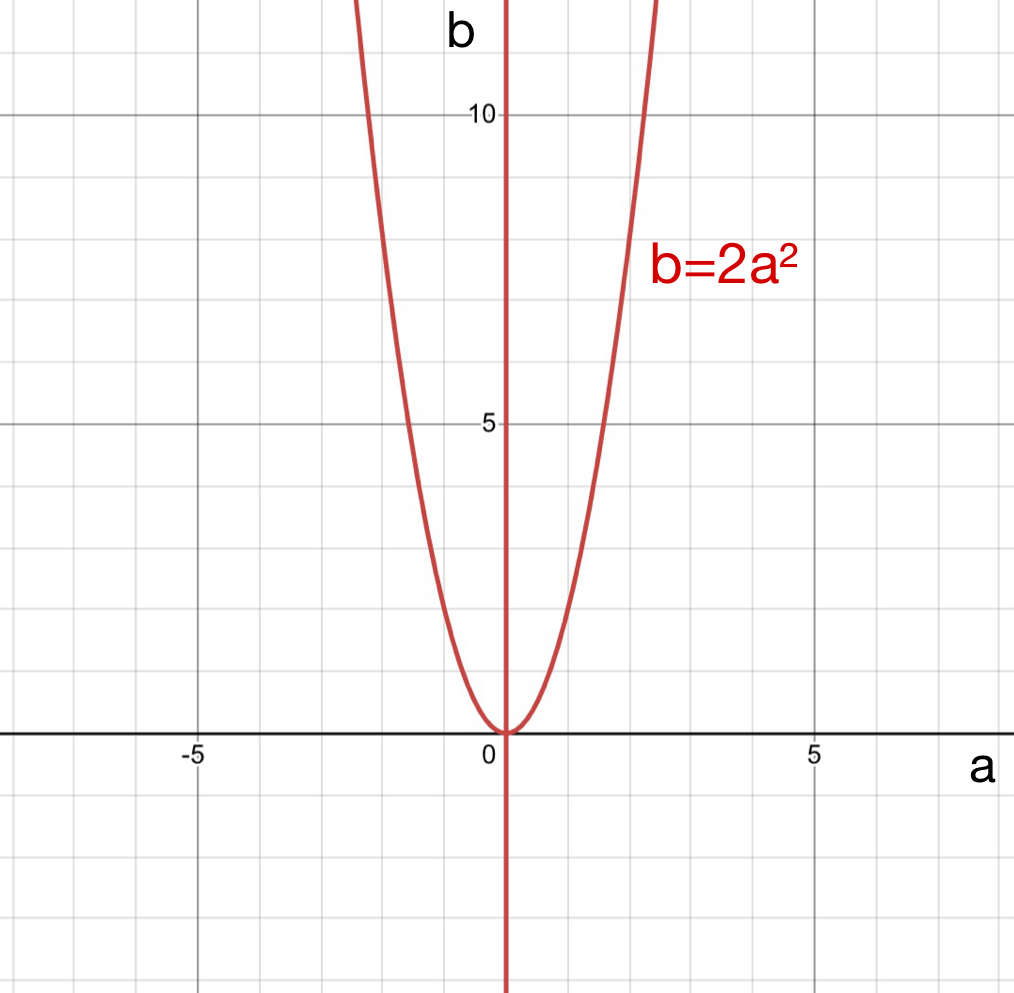
以上から, 条件を満たすような\((a, b)\)は, \(a=0\), または, \(b=2a^2\)であり, \((a, b)\)平面に図示すると以下のようになる.