今回はこちらの問題を解いていきます.
\(xy\) 平面上に原点を中心とする半径\(3\)の円\(C_1\)と, 直線\(x=2\)上をくまなく動く点\(\mathrm{P}\)を中心とする半径1の円\(C_2\)がある.
このとき, 以下の問いに答えよ.
(1) \(C_1\), \(C_2\)が\(2\)つの共有点をもつような\(\mathrm{P}\)の\(y\)座標の範囲を求めよ.
(2) \(C_1\), \(C_2\)が\(2\)つの共有点をもつとき, その\(2\)つの共有点を通る直線\(l\)に関して\(\mathrm{P}\)と対称な点を\(\mathrm{Q}\)とする. ただし, \(\mathrm{P}\)がその直線上にあるときは, \(\mathrm{P}=\mathrm{Q}\)とする. \( \mathrm{P}\)の\(y\)座標が(1)で求めた範囲を動くとき, \( \mathrm{Q} \)の軌跡を求めよ.
(2025 一橋大学 [2])
こちらはかなりの難問です. 計算量が多く, 文字式の割り算では都度分母が0にならないことの確認が必要です. 最終的には軌跡を求める問題ですが, 十分性もきちんと示す必要があります.
それでは解いていきましょう.
(1) \( \mathrm{P} \)の\(y\)座標を\(t\)とすると, \(C_2\)の中心は\((2, t)\)となるので, \(C_1\), \(C_2\)の中心間の距離\(d\)は,
$$
d=\sqrt{2^2+t^2}=\sqrt{t^2+4}
$$となる. \(C_1\)の半径は\(3\), \(C_2\)の半径は\(1\)であるから, \(C_1\), \(C_2)\)が共有点を\(2\)つもつ必要十分条件は,
$$
|3-1|<d<3+1
$$である. これを同値変形していくと,
$$
\begin{align}
&|3-1|<d<3+1\\[1.5ex]
&\iff 2<\sqrt{t^2+4}<4\\[1.5ex]
&\iff 2< \sqrt{t^2+4} \,\,\,\, かつ \,\, \sqrt{t^2+4}<4
\end{align}
$$最後の2つの不等式において, いずれも両辺正なので2乗しても同値関係が崩れないから
$$
\begin{align}
&2< \sqrt{t^2+4} \,\,\,\, かつ \,\, \sqrt{t^2+4}<4\\[1.5ex]
&\iff 4<t^2+4 \,\,\,\, かつ \,\, t^2+4<16
\end{align}
$$となる. まず, \(4<t^2+4\)に関しては,
$$
\begin{align}
&4<t^2+4 \\[1.5ex]
&\iff t^2>0 \\[1.5ex]
&\iff t\neq 0
\end{align}
$$である. 次に, \(t^2+4<16\)に関しては,
$$
\begin{align}
& t^2+4<16 \\[1.5ex]
&\iff t^2<12 \\[1.5ex]
&\iff -2\sqrt{3}<t<2\sqrt{3}
\end{align}
$$となる.
よって, 2つの不等式を同時に満たす,
$$
-2\sqrt{3}<t<0 \,\, \,\, または \,\, 0<t<2\sqrt{3}
$$が求める\(\mathrm{P}\)の\(y\)座標の範囲である.
(2) (1)に引き続き\( \mathrm{P} \)の\(y\)座標を\(t\)とし, \(t\)は(1)で求めた\(C_1\), \(C_2\)が\(2\)つの共有点をもつ範囲, \(-2\sqrt{3}<t<0 \,\, \,\, または \,\, 0<t<2\sqrt{3}\) を動くとする.
このとき, 任意の実数\(k\)に対して,
$$
k\left(x^2+y^2-3^2\right)+\left\{(x-2)^2+(y-t)^2-1^2\right\}=0
$$は, \(C_1\), \(C_2\)の\(2\)つの共有点を通る曲線である. 特に, \(k=-1\)とすることで,
$$
\begin{align}
&-\left(x^2+y^2-3^2\right)+\left\{(x-2)^2+(y-t)^2-1^2\right\}=0\\
&4x+2ty-t^2-12=0
\end{align}
$$ は直線となり, これが\(2\)つの共有点を通る直線\(l\)である.
まず, \(\mathrm{P}(2, t)\)が直線\(l\)上にあるとき,
$$
4\cdot 2+2t\cdot t-t^2-12=0
$$より, \(t=\pm2\)である. このとき, \(\mathrm{P}=\mathrm{Q}\)であり, \(t=2\)のとき\( \mathrm{Q} \)の座標は\((2,2)\), \(t=-2\)のとき\( \mathrm{Q} \)の座標は\((2,-2)\)となる.
次に\(\mathrm{P}\)が直線\(l\)上にないとき, つまり\(t\neq \pm2\)のときを考える. \(\mathrm{Q}\)の座標を\((X, Y)\)とすると, \(\mathrm{P}\), \(\mathrm{Q}\)の中点\( \displaystyle \left(\frac{2+X}{2}, \frac{t+Y}{2}\right) \)は\(l\)上にあることから,
$$
\begin{align}
&4\cdot \frac{2+X}{2}+2t\cdot \frac{t+Y}{2} -t^2-12=0\\[1.5ex]
&\iff 2X+tY=8 \,\,\,・・・①
\end{align}
$$である. また, 直線\(\mathrm{PQ}\)と直線\(l\)は直交するから, 直線\(\mathrm{PQ}\), 直線\(l\)の傾きをかけると\(-1\) になる. \(t\neq 0\)より, 直線\(l\)の傾きは\(\displaystyle -\frac{2}{t} \)となる. また, 直線\(l\)の傾きが\(0\)にないため, 直線\(l\)は\(x\)軸と平行にならない. よって, \(\mathrm{P}\)と\(\mathrm{Q}\)の\(x\)座標が一致することがなく, \(X\neq 2\)となり, 直線\(\mathrm{PQ}\)の傾きは, \( \displaystyle \frac{Y-t}{X-2} \)としてよい. これから,
$$
\begin{align}
&\frac{Y-t}{X-2}\cdot \left(-\frac{2}{t}\right)=-1\\[1.5ex]
&\iff tX=2Y \,\,\,・・・②
\end{align}
$$となる. ②より, \(\displaystyle Y=\frac{t}{2}X \)を①に代入して,
$$
\begin{align}
&2X+\frac{t^2}{2}X=8\\[1.5ex]
&\iff X=\frac{16}{t^2+4}
\end{align}
$$となり, \(Y\)についても,
$$
Y=\frac{t}{2}X=\frac{8t}{t^2+4}
$$と求まる. なお, \(t=2\)のとき, \((X,Y)=(2, 2)\), \(t=-2\)のとき, \((X,Y)=(2,-2)\)となるから, これは先に求めた\(\mathrm{P}\)が直線\(l\)上にある場合も含む.
よって, \(-2\sqrt{3}<t<0 \,\, \,\, または \,\, 0<t<2\sqrt{3}\) のとき, \(\mathrm{Q}\)の座標は, \(\displaystyle (X,Y)= \left(\frac{16}{t^2+4}, \frac{8t}{t^2+4}\right)\)となる.
つぎにこの\(\mathrm{Q} \)の軌跡を求める. \(\displaystyle X=\frac{16}{t^2+4}\neq 0\)であり, \(\displaystyle Y=\frac{t}{2}X\)から, \(\displaystyle t=\frac{2Y}{X}\)となる. これを\(\displaystyle X=\frac{16}{t^2+4}\)に代入して,
$$
\begin{align}
&X=\frac{16}{\left(\frac{2Y}{X}\right)^2+4}\\[1.5ex]
&\iff X\left(\frac{2Y}{X}\right)^2+4X=16\\[1.5ex]
&\iff 4Y^2+4X^2=16X\\[1.5ex]
&\iff Y^2+X^2=4X\\[1.5ex]
&\iff (X-2)^2+Y^2=2^2
\end{align}
$$となる. また, \(0<t^2<12\)であり, \(\displaystyle X=\frac{16}{t^2+4}\)であることから,
$$
\begin{align}
&0<t^2<12\\[1.5ex]
&\iff 4<t^2+4<16\\[1.5ex]
&\iff \frac{1}{16}<\frac{1}{t^2+4}<\frac{1}{4}\\[1.5ex]
&\iff 1<\frac{16}{t^2+4}<4\\[1.5ex]
&\iff 1<X<4
\end{align}
$$となり, \(X\)は\(1<X<4\)を満たす必要がある. 以上から, \(\mathrm{Q}\)は\((2,0)\)を中心とする半径\(2\)の円周上で, \(x\)座標が\(1<x<4\)を満たす範囲を動くことがわかる.
逆に, 点\(\mathrm{R}(a, b)\)が\((2,0)\)を中心とする半径\(2\)の円周上で, \(x\)座標が\(1<x<4\)を満たす範囲の点であるとき, \(b>0\)ならば,
$$
t=\sqrt{\frac{16}{a}-4}
$$とし, \(b<0\)ならば,
$$
t=-\sqrt{\frac{16}{a}-4}
$$とすることで, \(\mathrm{Q}\)が\(\mathrm{R}\)と一致することが次のように示される.
まず, \(1<a<4\)であるから, 上のようにして決めた\(t\)は
$$
-2\sqrt{3}<t<0 \,\, \,\, または \,\, 0<t<2\sqrt{3}
$$を満たことがわかり, \(t\)に対して\(\mathrm{Q}\)の座標を求める. まず, \(t>0\)のとき,
$$
\begin{align}
X&=\frac{16}{t^2+4}=\frac{16}{\left(\sqrt{\frac{16}{a}-4}\right)^2+4}=a\\[1.5ex]
Y&=\frac{t}{2}X=\frac{a}{2}\sqrt{\frac{16}{a}-4}=\sqrt{4a-a^2}=b
\end{align}
$$となる. ここで, \(t>0\)のとき, \(b>0\)になること, また, \((a, b)\)が\((a-2)^2+b^2=4\)を満たすことから\(b=\sqrt{4a-a^2}\)であることを用いた. また, \(t<0\)でも全く同様に\(X=a\), \(Y=b\)となることが示される.
以上から, \(Q\)の軌跡は, \((2,0)\)を中心とする半径\(2\)の円周上で, \(x\)座標が\(1<x<4\)を満たす部分となることがわかった. 図示すると以下の通りである.
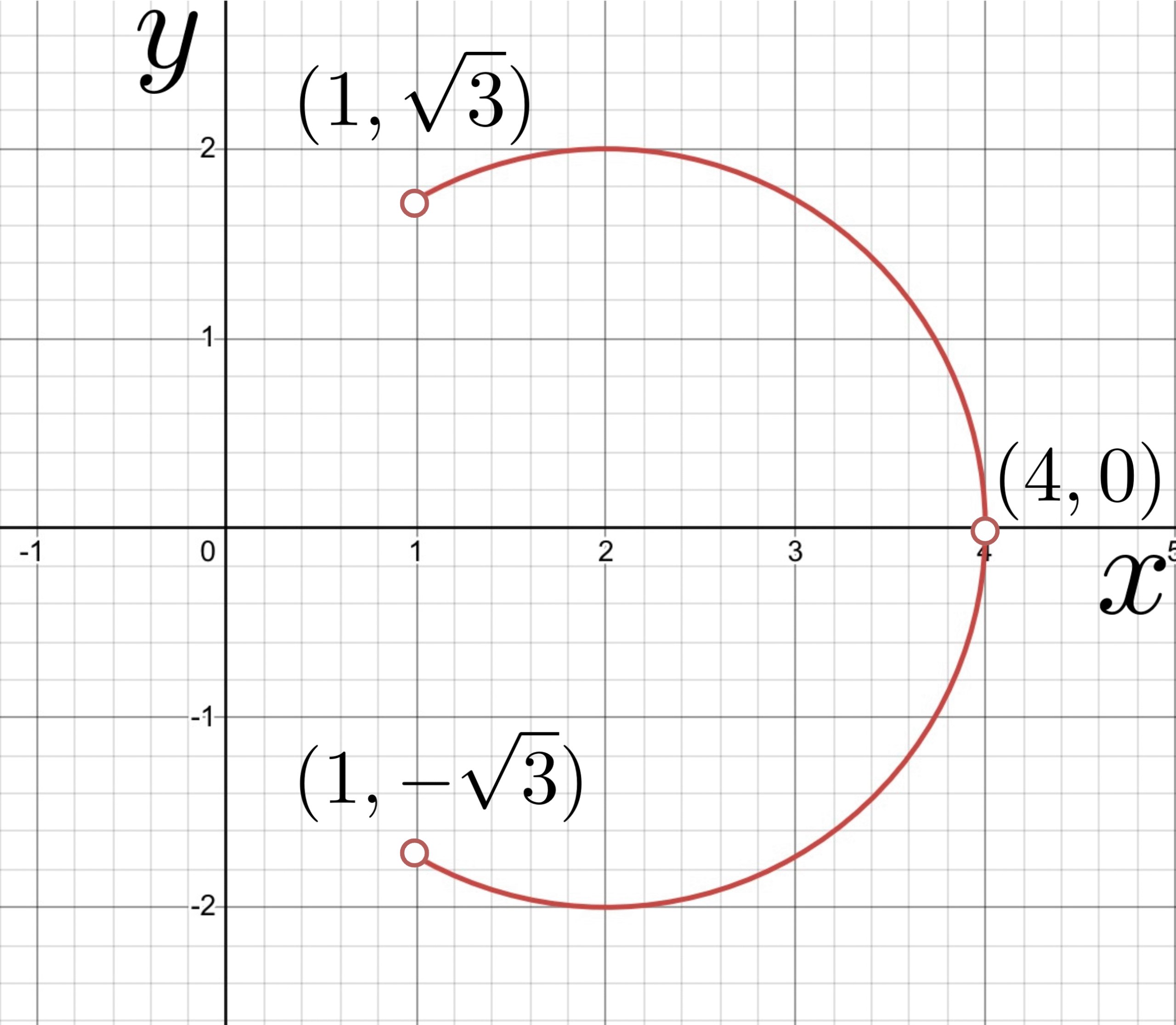
youtubeでも解説しています.