今回はこちらの問題を解いていきます.
\(n\)番目の素数を\(p_n\)で表す. 例えば, \(p_1=2\), \(p_2=3\), \(p_3=5\)である.
このとき, 以下の問いに答えよ.
(1) \(p_{15}\)を求めよ.
(2) \(n\geq 12\)のとき, \(p_n>3n\)を示せ.
(2024 大阪大学 [3])
素数の大きさを評価する問題です. 実は大学で学ぶ素数定理を用いることで, 任意の自然数\(k\)に対して, ある整数\(N\)が存在して,
$$
n\geq N\,\,\Longrightarrow p_n>kn
$$が成り立つことが示ます. 今回の問題では, \(k=3\)のときで, そのときの\(N\)が\(12\)ということです. この話は解答後におまけで記載することにします.
それでは解いていきましょう.
(1) 素数を小さい順に並べると,\(p_1=2\), \(p_2=3\), \(p_3=5\), \(p_4=7\), \(p_5=11\), \(p_6=13\), \(p_7=17\), \(p_8=19\), \(p_9=23\), \(p_{10}=29\), \(p_{11}=31\), \(p_{12}=37\), \(p_{13}=41\), \(p_14=43\), \(p_{15}=47\)となり,
$$
p_{15}=47
$$である.
(2) \(n\)に関する数学的帰納法で証明する.
① \(n=12\)のとき成り立つことを示す.
これは\(p_{12}=37 > 36=3\cdot 12\)より成り立つ.
② \(n=k\)のとき成り立つと仮定して, \(n=k+1\)のときも成り立つことを示す.
\(n=k\)のとき, 成り立つと仮定する. つまり, \(p_k>3k\)が成り立つとすると, \(p_k\)は自然数であるから, \(p_k\geq 3k+1\)である. 連続する自然数は片方が偶数(\(2\)で割れる)になるため, \(p_1=2\), \(p_2=3\)を除いて, 連続する自然数が素数になることはないから, \(p_{k+1}\geq p_k + 2\)である. よって,
$$
p_{k+1}\geq p_k+2\geq (3k+1)+2=3(k+1)
$$である. しかし, \(3(k+1)\)は\(3\)の倍数であるから, \(k=0\)を除いて素数にはなり得ない. よって\(p_{k+1}\neq 3(k+1)\)となり,
$$
p_{k+1}>3(k+1)
$$ がわかる.
①, ②より数学的帰納法から, \(n\geq 12\)のとき, \(p_n>3n\)が成り立つことが示された.
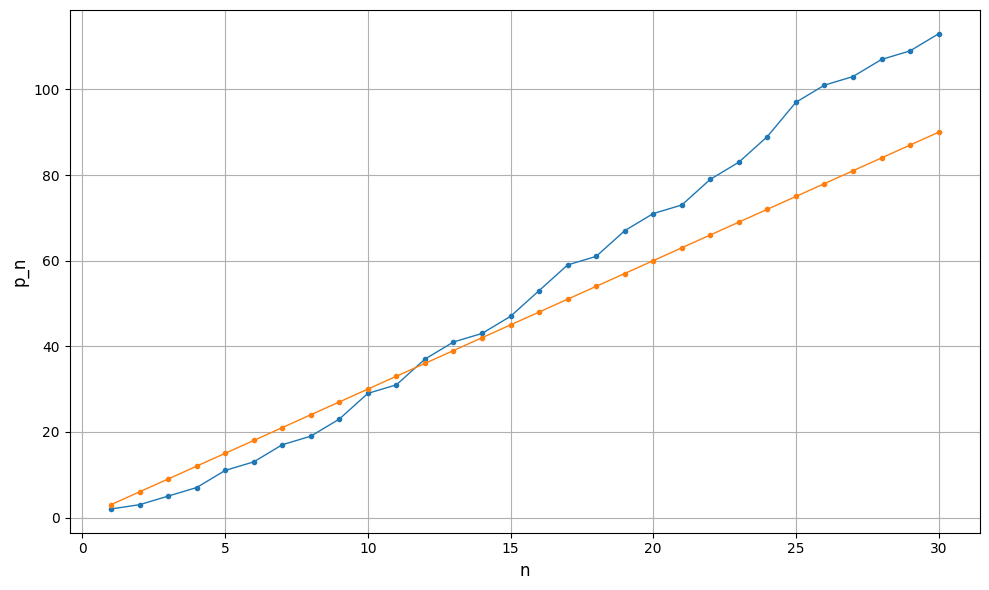
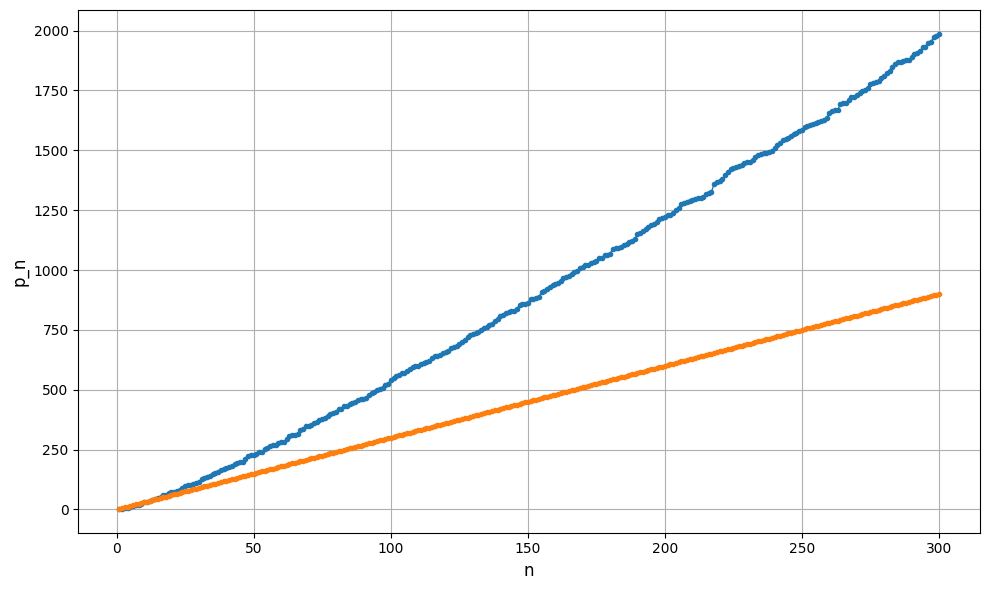
実際に, 横軸を\(n\)とし, \(p_n\), \(3n\)のグラフを描くと以下のようになります. たしかに, \(n\geq 12\)の範囲で, \(p_n>3n\)がわかります.
任意の自然数\(k\)に対して, ある整数\(N\)が存在して,
$$
n\geq N\,\,\Longrightarrow p_n>kn
$$が成り立つことを素数定理を使ってざっくりとした証明をしてみましょう. まず素数定理を紹介します.
\(\pi(x)\)を\(x\)以下の素数の個数を返す関数と定義すると, 十分大きい自然数\(n\)に対して,
$$
\pi(x)\sim \frac{x}{\log{x}}
$$となる.
それではこの素数定理を使ってざっくりとした証明をしていきます.
自然数\(n\)に対して\(\pi(p_n)=n\)であるから, 十分大きい\(n\)に対して, 素数定理から,
$$
n\sim \frac{p_n}{\log{p_n}}
$$となり,
$$
p_n\sim n\log{p_n}
$$である. ここで, 明らかに\(p_n\geq n\)であるから,
$$
p_n\sim n\log{p_n} \geq n\log{n}
$$となる. 任意の\(k\)に対して, \(n\)を十分大きくとれば,
$$
k<\log{n}
$$とできるので, 以上から,
$$
p_n\sim n\log{p_n} \geq n\log{n} > kn
$$となる.
こちらの証明は曖昧な議論もあるため完全な証明ではないことを注意しておきます.
youtubeでも解説しています.