今回はこちらの問題を解いていきます.
正の定数\(k\)に対して, 2つの曲線\(y=kx^2\)と\(y=x(x-2)^2\)で囲まれる2つの領域の面積が等しくなるように\(k\)の値を定めよ.
(2025 東北文系[4])
「交点を求めてそれぞれ積分して面積を出す」という方針はすぐに立ちますが, 直接計算しようとするととても大変です. 短時間で, 計算ミスなく正確に解くためには, 以下の解答のような工夫が必要です.
グラフを描いてみるとこのようになります. \(k\)の値によって放物線の開き具合が変わり, 2つの領域の面積も変化します.
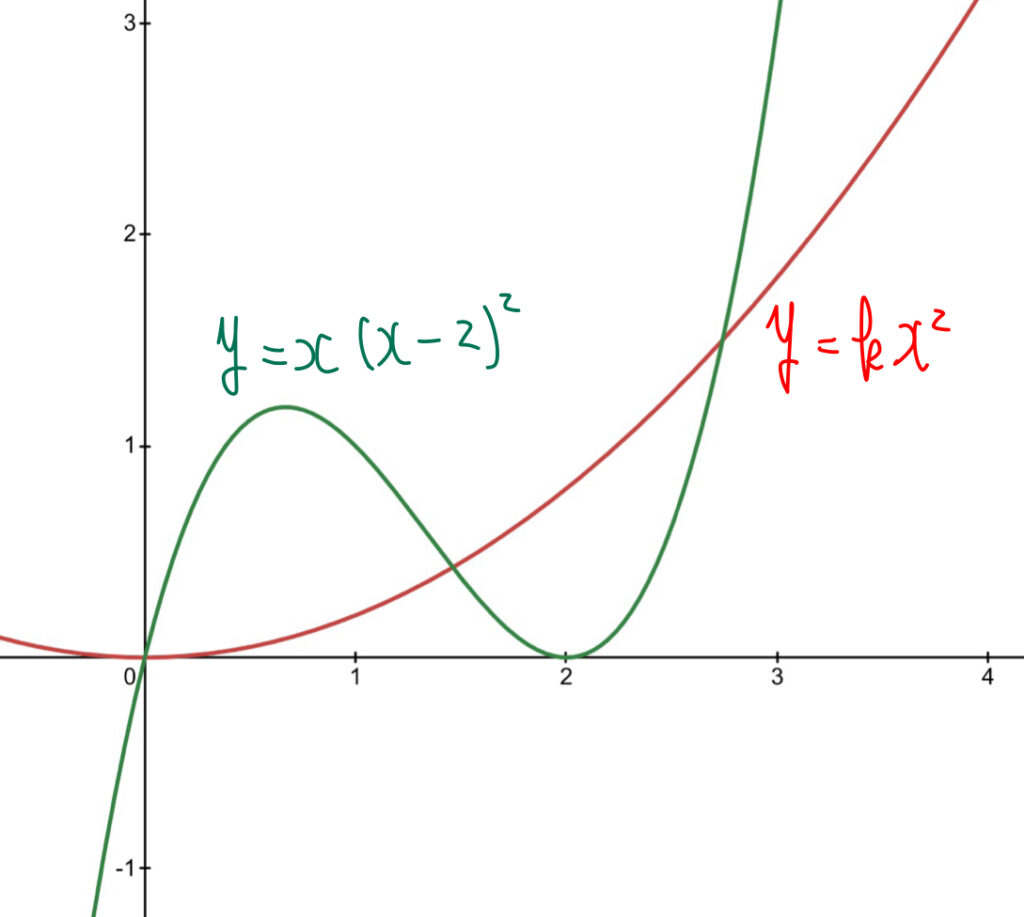
それでは解いていきましょう.
\(f(x)=kx^2\), \(g(x)=x(x-2)^2\)とおき, 2つの曲線\(y=f(x)\)と\(y=g(x)\)の共有点を求める. この2式から\(y\)を消去して\(x\)の3次方程式を解くと,
$$
\begin{align}
&kx^2=x(x-2)^2\\[1.5ex]
\iff &x(x-2)^2-kx^2=0\\[1.5ex]
\iff &x\left(x^2-4x+4-kx\right)=0\\[1.5ex]
\iff & x=0\,\,\,または\,\,\,x^2-(k+4)x+4=0
\end{align}
$$ となる. ここで2次方程式\(x^2-(k+4)x+4\)はその判別式\(D\)とすると,
$$
D=(k+4)^2-4\cdot 4=k^2+16k
$$となり, \(k>0\)であることから\(D>0\)となる. つまり2次方程式は相異なる2つの実数解\(x=\alpha, \beta\)をもつ. 解と係数の関係から,
$$
\begin{align}
\alpha+\beta&=k+4\,\,(>0) \,\, ・・・①\\[1.5ex]
\alpha\beta&=4\,\,(>0) \,\, ・・・②
\end{align}
$$であるから, \(\alpha\)と\(\beta\)は共に正であり, \(\alpha<\beta\)としても一般性を失わない.
以上から, 2つの曲線は3点で交わり, その\(x\)座標は小さい方から\(0\), \(\alpha\), \(\beta\)である. グラフからこの2曲線が囲む2つの領域の面積\(S_1\), \(S_2\)はそれぞれ,
$$
\begin{align}
S_1&=\int_0^\alpha\left\{g(x)-f(x)\right\}\,dx\\[1.5ex]
S_2&=\int_\alpha^\beta\left\{f(x)-g(x)\right\}\,dx
\end{align}
$$とかける. 問題の条件から\(S_1=S_2\)のとき,
$$
\begin{align}
S_1=S_2 &\iff \int_0^\alpha\left\{g(x)-f(x)\right\}\,dx = \int_\alpha^\beta\left\{f(x)-g(x)\right\}\,dx\\[1.5ex]
& \iff \int_0^\alpha\left\{g(x)-f(x)\right\}\,dx – \int_\alpha^\beta\left\{f(x)-g(x)\right\}\,dx=0\\[1.5ex]
& \iff \int_0^\alpha\left\{g(x)-f(x)\right\}\,dx + \int_\alpha^\beta\left\{g(x)-f(x)\right\}\,dx=0\\[1.5ex]
& \iff \int_0^\beta \left\{g(x)-f(x)\right\}\,dx=0
\end{align}
$$となるので, これを解いて\(k\)を求める.
$$
\begin{align}
\int_0^\beta \left\{g(x)-f(x)\right\}\,dx&=\int_0^\beta \left\{x(x-2)^2-kx^2\right\}\,dx\\[1.5ex]
&=\int_0^\beta \left\{x^2-(k+4)x+4\right\}\,dx\\[1.5ex]
&=\int_0^\beta x(x-\alpha)(x-\beta)\,dx\\[1.5ex]
&=\int_0^\beta \left\{x^2-(\alpha+\beta)x+\alpha\beta\right\}\,dx\\[1.5ex]
&=\int_0^\beta \left\{x^3-(\alpha+\beta)x^2+\alpha\beta x\right\}\,dx\\[1.5ex]
&=\left[\frac{1}{4}x^4-\frac{\alpha+\beta}{3}x^3+\frac{\alpha\beta}{2}x^2\right]_0^\beta\\[1.5ex]
&=\frac{1}{4}\beta^4-\frac{\alpha+\beta}{3}\beta^3+\frac{\alpha\beta}{2}\beta^2=0
\end{align}
$$最後に得られた\(\alpha\)と\(\beta\)の方程式にて, 両辺を\(\beta^3\neq 0\)で割って計算を続ける.
$$
\begin{align}
&\frac{1}{4}\beta^4-\frac{\alpha+\beta}{3}\beta^3+\frac{\alpha\beta}{2}\beta^2=0\\[1.5ex]
\iff & \frac{1}{4}\beta-\frac{\alpha+\beta}{3}+\frac{\alpha}{2}=0\\[1.5ex]
\iff & 3\beta-4\left(\alpha+\beta\right)+6\alpha=0\\[1.5ex]
\iff & -\beta+2\alpha=0\\[1.5ex]
\iff & \beta=2\alpha
\end{align}
$$となる. ここで, ①の\(\alpha\beta=4\)に, 上の\(\beta=2\alpha\)を代入して,
$$
2\alpha^2=4 \iff \,\, \alpha^2=2
$$となり, \(\alpha>0\)であることから, \(\alpha=\sqrt{2}\)であることがわかる. また, これから\(\beta=2\sqrt{2}\)がわかり, ②の\(\alpha+\beta=k+4\)から,
$$
k=\alpha+\beta-4=3\sqrt{2}-4
$$として, \(k\)の値が決まる.
この問題のポイントは
・交点の\(x\)座標を\(k\)を用いて具体的に表さないこと
・代わりに解と係数の関係から交点の\(x\)座標の関係式を使うこと
・\(S_1\), \(S_2\)の面積を具体的に計算せず解答中のように1つの積分で表すこと
になるかと思います。上の2つを実際にやってみると計算が煩雑でとても手に負えないことがわかるでしょう.
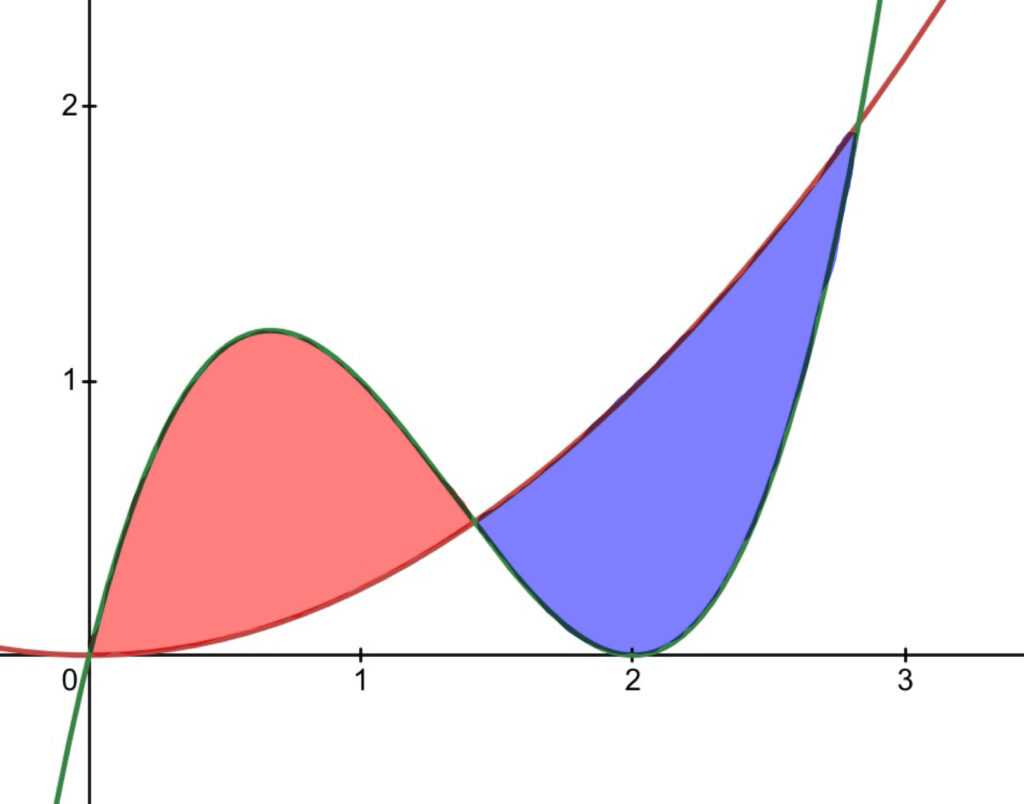
なお, \(k=3\sqrt{2}-4\)のときのグラフを書いてみると, たしかに2つの領域の面積が同じ大きになっていそうであることがわかります.
youtubeでも解説しています.