今回はこちらの問題を解いていきます.
半径\(1\)の円周上に2点\(\mathrm{A}\), \(\mathrm{B}\)を\(\mathrm{AB}=\sqrt{3}\)を満たすようにとる. このとき, 円周上を動く点\(\mathrm{P}\)に対して, \(\mathrm{AP}^2+\mathrm{BP}^2\)の最大値を求めよ.
(2025 九州大学文系[2])
適切に座標を設定し, \(\mathrm{AP}^2+\mathrm{BP}^2\)をパラメータで表せばすぐに解ける問題です. 今回は図形的な別解も添えてみました.
それでは解いていきましょう.
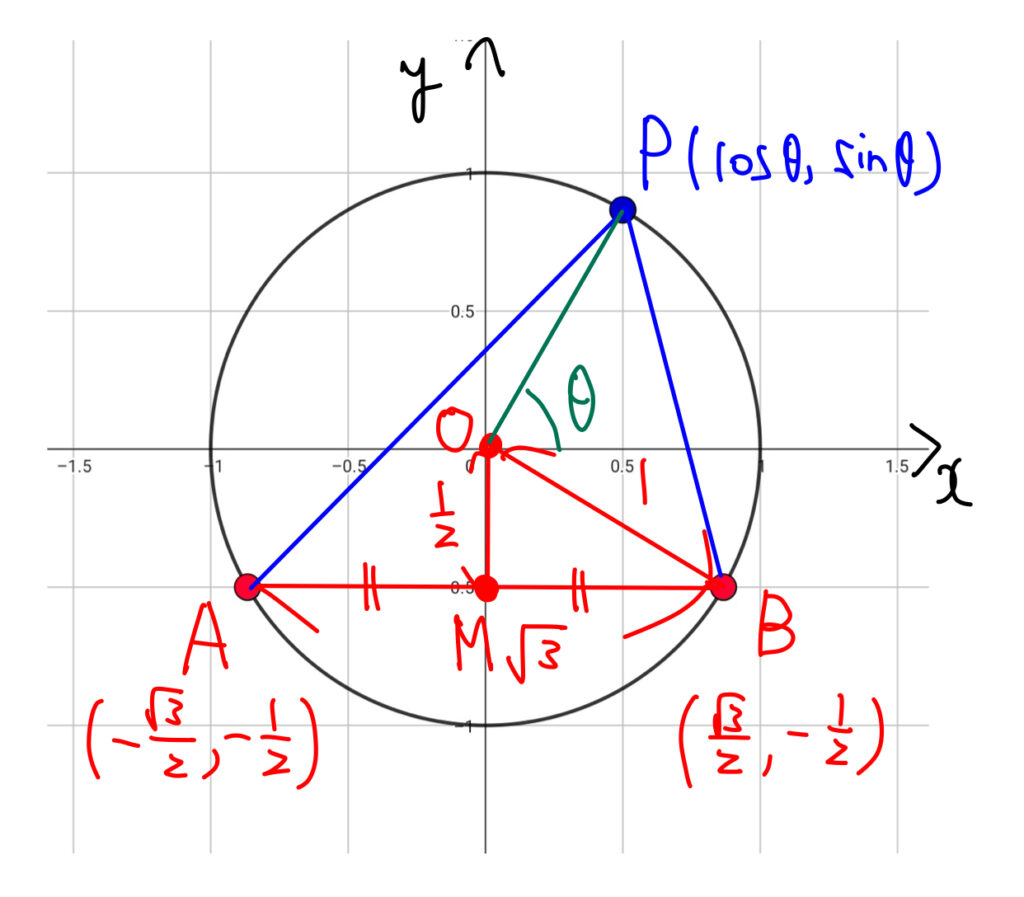
\(xy\)平面に原点\(\mathrm{O}\)を中心とする半径\(1\)の円を描き, 図のように円周上の2点\(\mathrm{A} \), \(\mathrm{B}\)を, 弦\(\mathrm{AB}\)が\(x\)軸に平行で\(x\)軸の下方に位置するように配置する. 弦\(\mathrm{AB}\)の中点を\(\mathrm{M}\)とすると, \(\displaystyle\mathrm{MB}=\frac{\sqrt{3}}{2}\), \(\mathrm{OB}=1\)であり, \(\triangle{\mathrm{OMB}}\)にて三平方の定理を用いることで, \(\displaystyle \mathrm{OM}=\frac{1}{2}\)がわかり, \(\displaystyle \mathrm{A} \left(-\frac{\sqrt{3}}{2},-\frac{1}{2}\right)\), \(\displaystyle \mathrm{B} \left(\frac{\sqrt{3}}{2},-\frac{1}{2}\right)\)となる. このように, \(\mathrm{A} \), \(\mathrm{B}\)を決めても一般性を失わない. また, 円周上の点\(\mathrm{P} \)に対して, \(x\)軸の正の向きから\(\mathrm{OP}\)まで反時計回りに測った角の大きさを\(\theta\)とする. \(\theta\)の範囲は\(0^\circ\leq\theta<{360}^\circ\)であり, \(\mathrm{P}\)の座標は\((\cos{\theta}, \sin{\theta})\)である.
以上の設定より,
$$
\begin{align}
\mathrm{AP}^2+\mathrm{BP}^2&=\left(\cos{\theta}-\left(-\frac{\sqrt{3}}{2}\right)\right)^2+\left(\sin{\theta}-\left(-\frac{1}{2}\right)\right)^2\\[1.5ex]
&+\left(\cos{\theta}-\frac{\sqrt{3}}{2}\right)^2+\left(\sin{\theta}-\frac{1}{2}\right)^2\\[1.5ex]
&=\cos^2{\theta}+\sqrt{3}\cos{\theta}+\frac{3}{4}+\sin^2{\theta}+\sin{\theta}+\frac{1}{4}\\[1.5ex]
&+\cos^2{\theta}-\sqrt{3}\cos{\theta}+\frac{3}{4}+\sin^2{\theta}+\sin{\theta}+\frac{1}{4}\\[1.5ex]
&=4+2\sin{\theta}
\end{align}
$$と求まる.
ここで, \(\sin{\theta}\)は\(\displaystyle \theta={90}^\circ\)のとき, 最大値を取るから, \(\mathrm{AP}^2+\mathrm{BP}^2\)も\(\displaystyle \theta={90}^\circ\)のときに最大となり, その値は\(6\)であることがわかる.
座標平面上に適切に円, 点を配置することで, いとも簡単に解けました. ちなみに, \(\mathrm{AP}^2+\mathrm{BP}^2\)が最大になるのは, \(\mathrm{P}\)が下図の位置にあるときであり, これも直感からは明らかです.
解答があまりにも短かったので, もう少し幾何に寄せた別解を考えました.
(別解)
一般に, 平面上に2点\(\mathrm{A}\), \(\mathrm{B}\)があり, その中点を\(\mathrm{M}\)とする. このとき, 平面上の任意の点\(\mathrm{P}\)に対し,
$$
\mathrm{AP}^2+\mathrm{BP}^2=2\mathrm{MP}^2+\frac{1}{2}\mathrm{AB}^2\,\,・・・①
$$が成り立つ(証明は後述).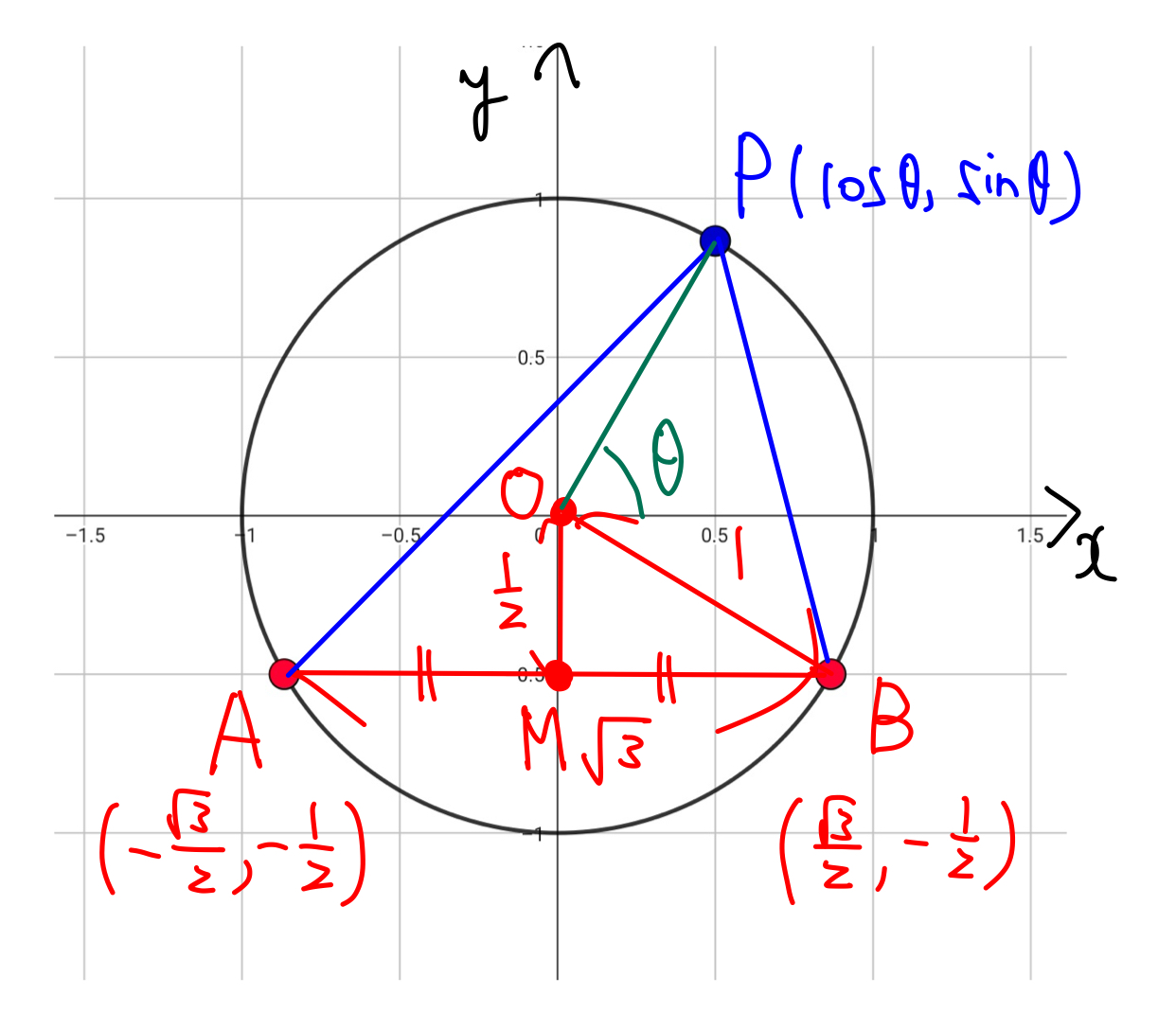
今回の問題では\(\mathrm{AB}=\sqrt{3}\)は固定だから, \(\mathrm{MP}\)が最大となるときに\(\mathrm{AP}^2+\mathrm{BP}^2\)もまた最大となる.
問題で与えられている半径\(1\)の円の中心を\(\mathrm{O}\)とするとき, 三角不等式から,
$$
\mathrm{MP}\leq \mathrm{OM} + \mathrm{OP}=\mathrm{OM} + 1
$$となり, 最右辺は\(\mathrm{P}\)に依らない一定値である. この不等式の統合が成立するのは, \(\mathrm{M}\), \(\mathrm{O}\), \(\mathrm{P}\)がこの順に1直線上に並ぶときである.
ここで, 以下の図から,
三平方の定理より,
$$
\mathrm{OM} = \sqrt{1^2 – \left( \frac{\sqrt{3}}{2} \right)^2} = \frac{1}{2}
$$であり, 同じく三平方の定理から,
$$
\begin{align}
\mathrm{AP}^2&=\mathrm{AM}^2+\mathrm{MP}^2=\left(\frac{\sqrt{3}}{2}\right)^2+\left(\frac{1}{2}+1\right)^2\\[1.5ex]
&=\frac{3}{4}+\frac{9}{4}=3
\end{align}
$$となり, 図の対称性から\(\mathrm{BP}^2=3\)である.
よって, \(\mathrm{AP}^2+\mathrm{BP}^2\)の最大値は\(3+3=6\)である.
別解中の①の証明を与えておきます.
(①の証明)
余弦定理より,
$$
\begin{align}
\mathrm{AP}^2=\mathrm{AM}^2+\mathrm{MP}^2-2 \mathrm{AM}\cdot \mathrm{MP}\cos{\angle{\mathrm{AMP}}}\\[1.5ex]
\mathrm{BP}^2=\mathrm{BM}^2+\mathrm{MP}^2-2 \mathrm{BM}\cdot \mathrm{MP}\cos{\angle{\mathrm{BMP}}}
\end{align}
$$である. ここで,
$$
\begin{align}
\cos \angle \mathrm{AMP} + \cos \angle \mathrm{BMP}
&= \cos \angle \mathrm{AMP} + \cos\left(180^\circ – \angle \mathrm{AMP} \right) \\[1.5ex]
&= \cos \angle \mathrm{AMP} – \cos \angle \mathrm{AMP} \\[1.5ex]
&= 0
\end{align}
$$であること, また, \(\displaystyle \mathrm{AM}=\mathrm{BM}=\frac{\mathrm{AB}}{2}\)であることに注意して両辺を足せば,
$$
\mathrm{AP}^2+\mathrm{BP}^2=\mathrm{AM}^2+\mathrm{BM}^2+2\mathrm{MP}^2=\frac{1}{2}\mathrm{AB}^2+2\mathrm{MP}^2
$$となる.
youtubeでも解説しています.