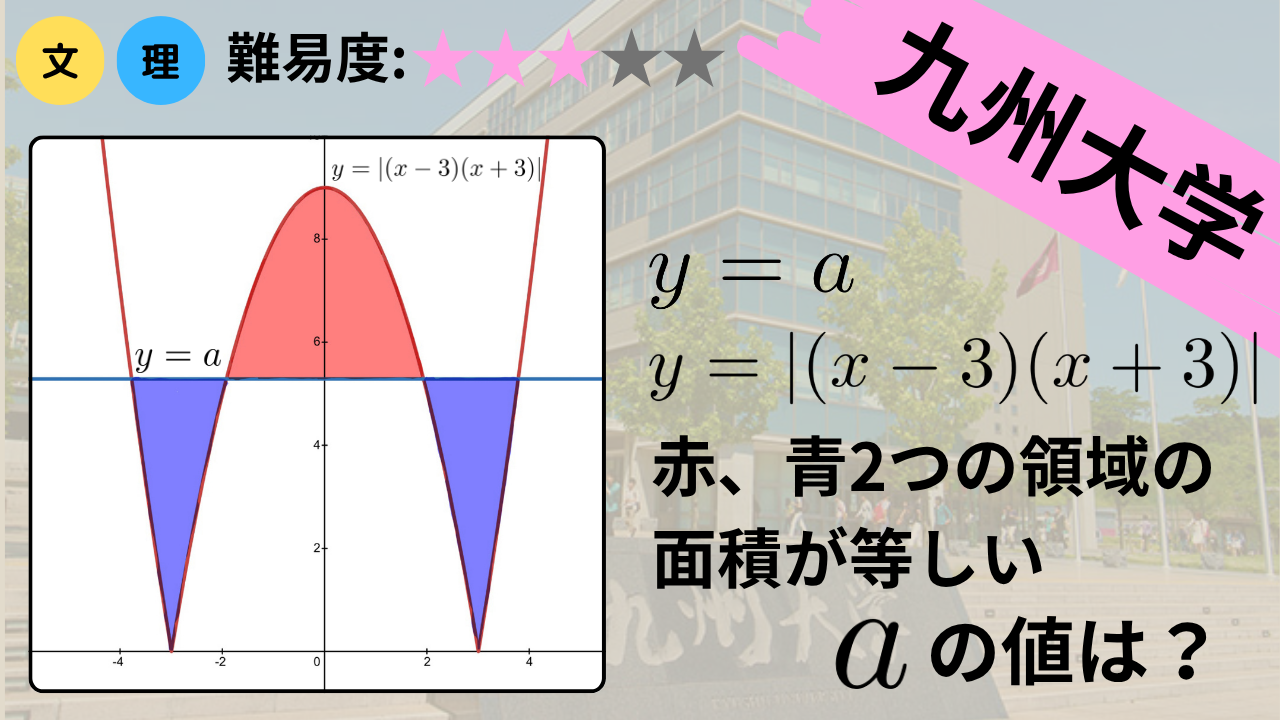
今回はこちらの問題を解いていきます.
\(a\)を\(0<a<9\)を満たす実数とする. 曲線\(C: y=|(x-3)(x+3)|\)と, 直線\(l: y=a\)で囲まれる図形のうち, \(y\geq a\)の領域にある部分の面積を\(S_1\), \(y\leq a\)の領域にある部分の面積を\(S_2\)とする. \(S_1=S_2\)となるときの, \(a\)の値を求めよ.
(2023 九州大学 文系 [1])
対数の性質, 階差数列, 等比数列の和の公式をふんだんに使って解いていく問題ですが, 丁寧な誘導があるので, 難しくはありません.
それでは解いていきましょう.
\(xy\)平面に\(C\)と\(l\)を描くと以下のようになり, \(C\)と\(l\)は\(0<x<3\)と\(3<x\)の領域にそれぞれ1つずつ共有点を持つことがわかる. 共有点の\(x\)座標をそれぞれ\(\alpha\), \(\beta\)とする. ただし, \(0<\alpha<3<\beta\)である.
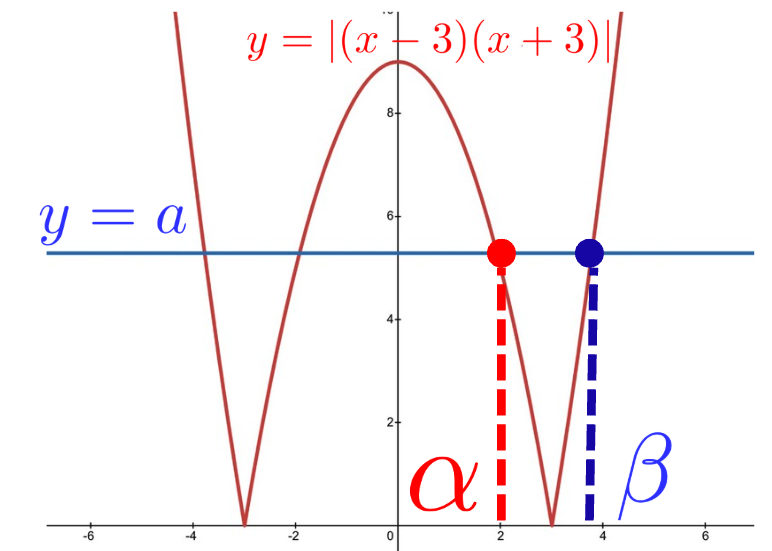
まず, \(\alpha\)を求めると, \(0<\alpha<3\)より, \(\alpha\)は以下の方程式の\(x>0\)における解となるから,
$$
\begin{align}
&-(x-3)(x+3)=a\\[1.5ex]
&\iff 9-x^2=a\\[1.5ex]
&\iff x^2=9-a
\end{align}
$$より,
$$
\alpha =\sqrt{9-a}
$$がわかる.
\(\beta\)については, \(\beta>3\)より, \(\beta\)は以下の方程式の\(x>0\)における解となるから,
$$
\begin{align}
&(x-3)(x+3)=a\\[1.5ex]
&\iff x^2-9=a\\[1.5ex]
&\iff x^2=9+a
\end{align}
$$より,
$$
\beta =\sqrt{9+a}
$$がわかる.
今回面積を求める2つの領域はそれぞれ\(y\)軸に関して対称であるため, 各領域で\(x\geq 0\)の領域に含まれる部分の面積の2倍が\(S_1\), \(S_2\)となる. \(9-a=\alpha^2\), \(9+a=\beta^2\)に注意して, 各面積を計算する. まず\(S_1\)は
$$
\begin{align}
S_1&=2\int_0^\alpha\left\{-(x-3)(x+3)-a\right\}\,dx\\[1.5ex]
&=2\int_0^\alpha\left(-x^2+9-a\right)\,dx\\[1.5ex]
&=2\int_0^\alpha\left(-x^2+\alpha^2\right)\,dx\\[1.5ex]
&=2 \left[-\frac{x^3}{3}+\alpha^2x\right]_0^\alpha\\[1.5ex]
&=2 \left(-\frac{\alpha^3}{3}+\alpha^3\right)\\[1.5ex]
&=\frac{4}{3}\alpha^3
\end{align}
$$となる.
次に\(S_2\)は領域を\(\alpha\leq x \leq 3\)と, \(3\leq x \leq \beta\)の2つの領域に分け, それぞれの領域の面積\(S_2^\prime\), \(S_2^{\prime\prime}\)を求め, それを足すことで求めることとする.
$$
\begin{align}
S_2^\prime &= 2\int_\alpha^3\left\{a+(x-3)(x+3)\right\}\,dx \\[1.5ex]
&= 2\int_\alpha^3\left(x^2+a-9\right)\,dx \\[1.5ex]
&= 2\int_\alpha^3\left(x^2-\alpha^2\right)\,dx \\[1.5ex]
&= 2\left[\frac{x^3}{3}-\alpha^2 x\right]_\alpha^3 \\[1.5ex]
&= 2\left(9-3\alpha^2-\frac{\alpha^3}{3} + \alpha^3\right) \\[1.5ex]
&= 2\left(9-3\alpha^2+\frac{2}{3}\alpha^3\right) \\[1.5ex]
\end{align}
$$
$$
\begin{align}
S_2^{\prime\prime} &= 2\int_3^\beta\left\{a-(x-3)(x+3)\right\}\,dx \\[1.5ex]
&= 2\int_3^\beta\left(-x^2+9+a\right)\,dx \\[1.5ex]
&= 2\int_3^\beta\left(-x^2 + \beta^2\right)\,dx \\[1.5ex]
&= 2\left[-\frac{x^3}{3} + \beta^2 x\right]_3^\beta \\[1.5ex]
&= 2\left(-\frac{\beta^3}{3} + \beta^3+9-3\beta^2\right)\\[1.5ex]
&= 2\left(\frac{2}{3}\beta^3 +9-3\beta^2\right)
\end{align}
$$
これから, $$
\begin{align}
S_2&=2\left(9-3\alpha^2+\frac{2}{3}\alpha^3\right)+2\left(\frac{2}{3}\beta^3 +9-3\beta^2\right)\\[1.5ex]
&=2 \left( 18-3(\alpha^2+\beta^2)+\frac{2}{3}\alpha^3 + \frac{2}{3}\beta^3 \right)\\[1.5ex]
&=2 \left( 18-3(9-a+9+a)+\frac{2}{3}\alpha^3 + \frac{2}{3}\beta^3 \right)\\[1.5ex]
&=2 \left( -36+\frac{2}{3}\alpha^3 + \frac{2}{3}\beta^3 \right)\\[1.5ex]
\end{align}
$$となる.
\(S_1=S_2\)として,
$$
\begin{align}
\frac{4}{3}\alpha^3&=2 \left( -36+\frac{2}{3}\alpha^3 + \frac{2}{3}\beta^3 \right)\\[1.5ex]
\frac{4}{3}\beta^3&=72\\[1.5ex]
\beta^3&=54\\[1.5ex]
\sqrt{9+a}&=\sqrt[3]{54}\\[1.5ex]
\sqrt{9+a}&=3\sqrt[3]{2}\,\,\,(両辺正より二乗して)\\[1.5ex]
9+a&=9\sqrt[3]{4} \\[1.5ex]
a&=9\left(\sqrt[3]{4}-1\right)
\end{align}
$$として\(a\)が求まった.
youtubeでも解説しています.