今回はこちらの問題を解いていきます.
3次関数\(f(x)=x^3-6x^2-15x+30\)について, 曲線\(C:y=f(x)\)を考える. 以下の問いに答えよ.
(1) \(f(x)\)の極値を求めよ.
(2) \(C\)上の点\((-3, -6)\)を通り, \(C\)に接する直線の方程式を全て求めよ.
(2025 北海道大学 文系[1])
この問題は教科書の例題レベルの超基本問題なので確実に解けるようになりましょう.
それでは解いていきましょう.
(1) \(f(x)=x^3-6x^2-15x+30\)を微分すると,
$$
f^\prime(x)=3x^2-12x-15=3(x^2-4x-5)=3(x-5)(x+1)
$$となり, \(f^\prime(x)=0\)とおくと, \(x=-1, 5\)となる. ここで, \(f(-1)=38\), \(f(5)=-70\)に注意して, 増減表を書くと,
$$
\begin{array}{|c|c|c|c|c|c|}
\hline
x & \cdots & -1 &\cdots & 5 & \cdots \\[1.5ex]
\hline
f'(x) & + & 0 & – & 0 & + \\[1.5ex]
\hline
f(x) & \nearrow & 38 & \searrow & -70 & \nearrow \\[1.5ex]
\hline
\end{array}
$$となる.
よってグラフは以下のようになり, \(f(x)\)は\(x=-1\)で極大値\(28\)を, \(x=5\)で極小値\(-20\)をとることがわかる.
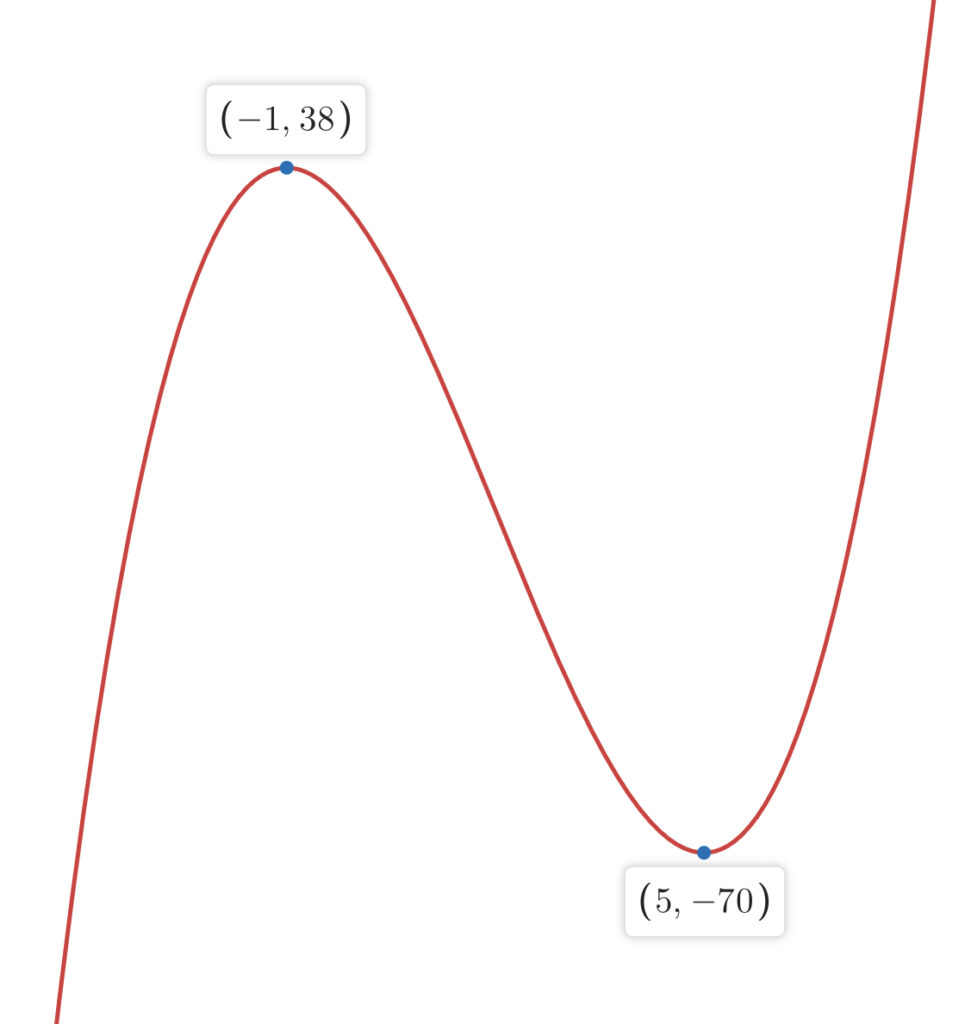
(2) 任意の実数\(a\)に対して, \(C\)の\(x=a\)における接線の方程式を求めると, これは傾きが\(f^\prime(a)\)で\((a, f(a))\)を通ることから,
$$
\begin{align}
y&=f^\prime(a)(x-a)+f(a)\\[1.5ex]
&=(3a^2-12a-15)(x-a)+a^3-6a^2-15a+30\\[1.5ex]
&=(3a^2-12a-15)x-2a^3+6a^2+30
\end{align}
$$となる. これが\((-3, -6)\)を通るから,
$$
\begin{align}
&-6=(3a^2-12a-15)\cdot(-3)-2a^3+6a^2+30\\[1.5ex]
&\iff 2a^3+3a^2-36a-81=0
\end{align}
$$として\(a\)の3次方程式が得られる. \(a=-3\)はこの方程式の1つの解であり, 左辺は\((a+3)\)を因子に持つことがわかる. これから方程式を変形すると,
$$
\begin{align}
&2a^3+3a^2-36a-81=0\\[1.5ex]
&\iff (a+3)(2a^2-3a-27)=0\\[1.5ex]
&\iff (a+3)^2(2a-9)=0
\end{align}
$$となり, この方程式の解は,
$$
\begin{align}
a&=-3\,\,(重解)\\[1.5ex]
a&=\frac{9}{2}
\end{align}$$であることがわかる. これから求める接線は, \(a=-3\)のとき,
$$
\begin{align}
y&=\left(3\cdot(-3)^2-12\cdot(-3)-15\right)x-2\cdot(-3)^3+6\cdot(-3)^2+30\\[1.5ex]
&=48x+138
\end{align}
$$であり, \( \displaystyle a=\frac{9}{2}\)のとき,
$$
\begin{align}
y&=\left(3\cdot\left(\frac{9}{2}\right)^2-12\cdot\left(\frac{9}{2}\right)-15\right)x-2\cdot\left(\frac{9}{2}\right)^3+6\cdot\left(\frac{9}{2}\right)^2+30\\[1.5ex]
&=-\frac{33}{4}x-\frac{123}{4}
\end{align}$$
となる.
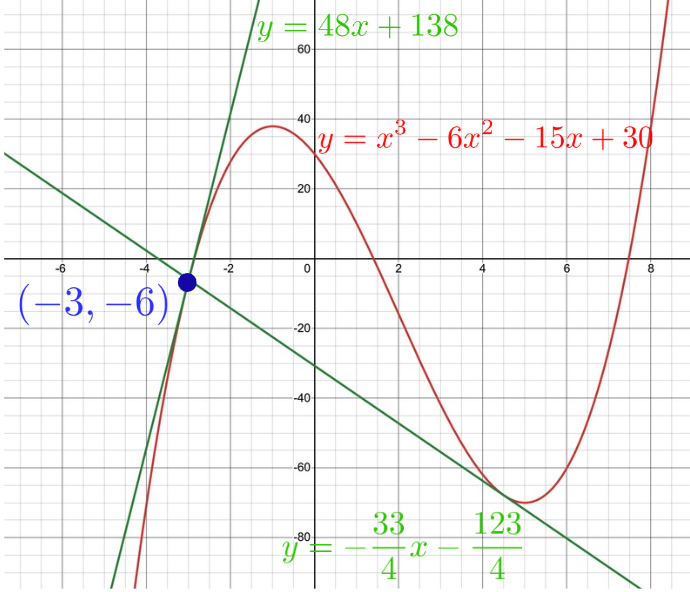
実際にグラフを描いてみると, 以下のようになり, 求めた2本の直線が\((-3, -6)\)を通り\(C\)に接することがわかります.
youtubeでも解説しています.








