今回はこちらの問題を解いていきます.
以下の問いに答えよ.
(1) \(x>1\), \(y>1\)のとき,
$$
\log_x{y}+\log_y{x}\geq 2
$$を示せ.
(2) 以下の連立不等式が表す領域を図示せよ.
$$
x>1,\,\,y>x\,\, \log_x{y}+\log_y{x}<\frac{5}{2}
$$
(3) (2)の領域でさらに\(x^2+y^2<12\)も満たす領域に境界線を含めた図形を\(D\)とする. \(D\)の面積を求めよ.
(2024 筑波大学 文系[2] 理系[2])
対数の入った不等式, そして不等式が定める領域の面積の問題です. 対数は符号がわかりにくく, 不等式操作などで間違ってしまうことが多いので, 注意して解きましょう. その上で, 符号を確認したことを答案に書かないと減点対象になるので気をつけましょう.
また, 面積を求める領域の一部に円が境界として現れます. 文系はルートの入った積分を扱わないため, 直接積分で求めることができません. そのことを考慮して解答を作成しています. 解答後に別解でルートの入った積分で面積を求める方法を紹介しています.
それでは解いていきましょう.
(1) \(\log_x{y}\), \(\log_y{x}\)について, \(x>1\), \(y>1\)であるから, これらはいずれも正である. よって, 相加相乗平均から,
$$
\log_x{y}+\log_y{x}\geq 2\sqrt{\log_x{y} \cdot \log_y{x}}
$$である. ここで, 底の変換公式から\(\log_y{x}\)の底を\(x\)に変換すると,
$$\log_y{x}=\frac{\log_x{x}}{\log_x{y}}=\frac{1}{\log_x{y}}
$$であるから,
$$
\log_x{y}+\log_y{x}\geq 2\sqrt{\log_x{y} \cdot \frac{1}{\log_x{y}}}=2
$$がわかる.
等号成立は,
$$
\log_x{y}=\log_y{x}
$$より,
$$
\log_x{y}=\frac{1}{\log_x{y}}
\iff \left(\log_x{y}\right)^2=1
$$が成り立つときである. \(\log_x{y}>0\)であるから, これは, \(\log_x{y}=1\)と同値であり, 結果, \(x=y\)のときであることがわかる.
(2) \(x>1\), \(y>x\)より, \(\log_x{y}>1\)であることに注意して, \(\log_x{y}+\log_y{x}<\frac{5}{2}\)を同値変形すると,
$$
\begin{align}
& \log_x{y}+\log_y{x}<\frac{5}{2}\\[1.5ex]
\iff & \log_x{y}+\frac{1}{\log_x{y}}<\frac{5}{2}\\[1.5ex]
\iff & 2\left(\log_x{y}\right)^2-5\log_x{y}+2<0\\[1.5ex]
\iff & (2\log_x{y}-1)(\log_x{y}-2)<0\\[1.5ex]
\iff & \frac{1}{2}<\log_x{y}<2\\[1.5ex]
\iff & 1<\log_x{y}<2\,\,(前提で, \log_x{y}>1 のため)
\end{align}
$$である. ここで,\(x>1\)より, \(a<b\)ならば\(x^a<x^b\)であるから, 最後の不等式より,
$$
\begin{align}
& \log_x{y}+\log_y{x}<\frac{5}{2}\\[1.5ex]
\iff & 1<\log_x{y}<2\\[1.5ex]
\iff & x^1<x^{\log_x{y}}<x^2\\[1.5ex]
\iff & x<y<x^2
\end{align}
$$よって, \(x>1\), \(y>x\)と合わせて領域を図示すると, 以下となる. ただし, いずれの境界線も含まない.
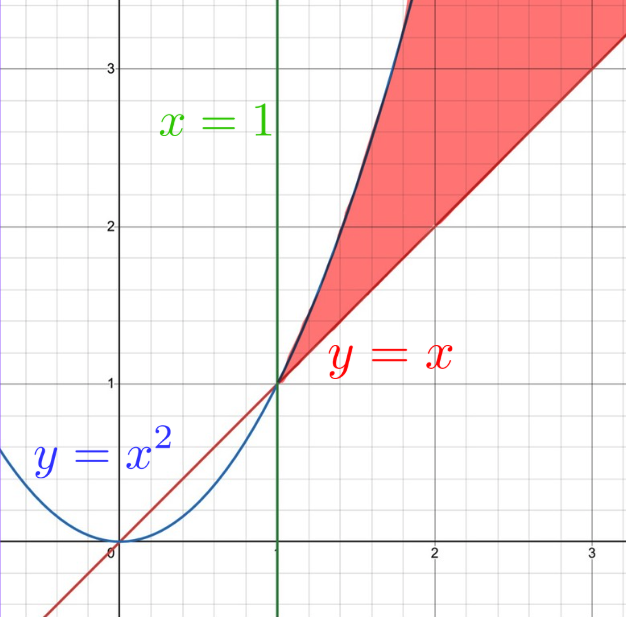
(3) \(x^2+y^2<12\)の条件を加え領域を図示すると, 以下の通りとなる. ここで, \(x^2+y^2<12\)の境界である円\(x^2+y^2=12\)と, \(y=x^2\), \(y=x\)の第一象限における交点をそれぞれ\(\mathrm{A}\), \(\mathrm{B}\)としている.
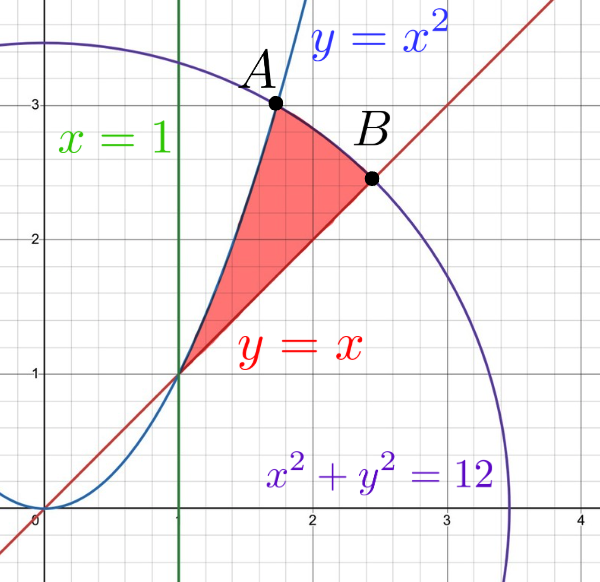
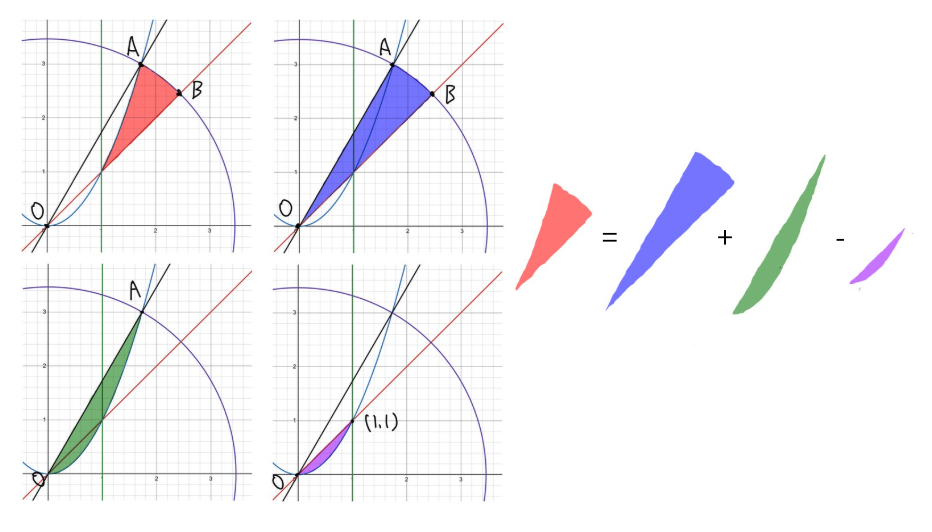
ここで\(\mathrm{O}\)と\(\mathrm{A}\)を直線で結び, 扇形\(\mathrm{OAB}\)を考える. このとき, 以下の図から求める領域Dの境界線を含めた面積\(S\)は,
$$
\begin{align}
S&= (扇形\mathrm{OAB}の面積)-(直線\mathrm{OA}とy=x^2で囲まれる領域の面積)\\
&+(y=xとy=x^2で囲まれる領域の面積)
\end{align}
$$となることがわかる.
まず扇形\(\mathrm{OAB}\)の面積\(S_1\)を求めるために, \(\mathrm{A}\)の座標を求める. これは, \(y=x^2\)と\(x^2+y^2=12\)を連立して, \(y\)を消去することで,
$$
\begin{align}
&x^2+\left(x^2\right)^2=12\\[1.5ex]
\iff &x^4+x^2-12=0\\[1.5ex]
\iff &(x^2+4)(x^2-3)=0\\[1.5ex]
\iff &x^2=3
\end{align}
$$ となる. ここで, \(\mathrm{A}\)は第一象限にあるので, \(x=\sqrt{3}\)がわかり, \(\mathrm{A}\)の座標は\((\sqrt{3}, 3)\)である.
これから直線\(\mathrm{OA}\)の傾きは\(\displaystyle \frac{3}{\sqrt{3}}=\sqrt{3}\)となり, 直線\(\mathrm{OA}\)が\(x\)軸の正の方向となす角の大きさは, \(\displaystyle \frac{\pi}{3}\)であることがわかる. さらに直線\(y=x\)が\(x\)軸の正の方向となす角の大きさは, \(\displaystyle \frac{\pi}{4}\)であるから, 扇形\(\mathrm{OAB}\)の中心角の大きさ\(\angle{\mathrm{OAB}}\)は,
$$
\angle{\mathrm{OAB}}=\frac{\pi}{3}-\frac{\pi}{4}=\frac{\pi}{12}
$$となる.
扇形\(\mathrm{OAB}\)は半径\(2\sqrt{3}(=\sqrt{12}\))の円から切り出されたものなので, その面積\(S_1\)は,
$$
S_1 = \pi(2\sqrt{3})^2\times\frac{\frac{\pi}{12}}{2\pi}=\frac{\pi}{2}
$$となる.
次に, 直線\(\mathrm{OA}(y=\sqrt{3}x)\)と\(y=x^2\), 直線\(y=x\)と\(y=x^2\)に囲まれた領域の面積\(S_2\), \(S_3\)をそれぞれ求める. これは積分から簡単に求まり,
$$
\begin{align}
S_2&=\int_0^{\sqrt{3}}{\sqrt{3}x-x^2}\,dx=\left[\frac{\sqrt{3}}{2}x^2-\frac{1}{3}x^3\right]_0^{\sqrt{3}}\\[1.5ex]
&=\frac{3\sqrt{3}}{2}-\sqrt{3}=\frac{\sqrt{3}}{2}\\[1.5ex]
S_3&=\int_0^1{x-x^2}\,dx=\left[\frac{\sqrt{x^2}}{2}-\frac{1}{3}x^3\right]_0^1\\[1.5ex]
&=\frac{\sqrt{1}}{2}-\frac{1}{3}=\frac{1}{6}
\end{align}
$$となる.
よって最終的に境界線を含めた領域\(D\)の面積\(S\)は,
$$
S=S_1-S_2+S_3=\frac{\pi}{2}-\frac{\sqrt{3}}{2}+\frac{1}{6}
$$と求まる.
先の解答はルートの入った積分を扱うことができない文系の方向けの解答でした. ルートが入った積分を使えないことから, 積分で円の一部と直線で囲まれる面積を求めることができないため, 既知の円や扇形の面積の公式を使って\(D\)の面積を求めていきました. この発想はなかなか気づきにくく難易度の高い問題ではないかと思っております.
理系であれば以下のように積分することで簡単に求めることができます.
(3)の別解 (理系, およびルートの入った積分を知っている文系向け)
まず, \(\mathrm{B}\)の座標を求める. これは, \(y=x\)と\(x^2+y^2=12\)を連立して, \(y\)を消去することで
$$
\begin{align}
&x^2+x^2=12\\[1.5ex]
&\iff x^2=6\\[1.5ex]
&\iff x=\pm\sqrt{6}
\end{align}
$$となり, \(\mathrm{B}\)は第一象限にあるので, \(x=\sqrt{6}\)となる. これから, \(\mathrm{B}\)の座標は\((\sqrt{6}, \sqrt{6})\)であることがわかる.
円\(x^2+y^2=12\)の\(x\)軸より上の部分は\(\displaystyle y=\sqrt{12-x^2}\)と表せるので, 境界を含めた領域\(D\)面積\(S\)は,
$$
\begin{align}
S&=\int_1^\sqrt{3}\left(x^2-x\right)\,dx+\int_\sqrt{3}^\sqrt{6}\left(\sqrt{12-x^2}-x\right)\,dx\\[1.5ex]
&=\int_1^\sqrt{3}\left(x^2-x\right)\,dx+\int_\sqrt{3}^\sqrt{6}{\sqrt{12-x^2}}\,dx-\int_\sqrt{3}^\sqrt{6}{x}\,dx
\end{align}
$$を計算すれば良い. 積分をそれぞれ計算する.
1つ目の積分は,
$$
\begin{align}
\int_1^\sqrt{3}\left(x^2-x\right)\,dx&=\left[\frac{\sqrt{x^3}}{3}-\frac{x^2}{2}\right]_1^\sqrt{3}\\[1.5ex]
&=\sqrt{3}-\frac{3}{2}-\frac{1}{3}+\frac{1}{2}\\[1.5ex]
&=\sqrt{3}-\frac{4}{3}
\end{align}
$$と計算できる.
2つ目の積分は, \(x=2\sqrt{3}\sin{\theta}\)として置換積分を行う. 積分範囲は,
$$
\begin{array}{c|ccc}
x & \sqrt{3} & \rightarrow & \sqrt{6} \\
\hline
\theta & \frac{\pi}{6} & \rightarrow & \frac{\pi}{4} \\
\end{array}
$$であり,
$$
dx=2\sqrt{3}\cos{\theta}d\theta
$$となるから,
$$
\begin{align}
\int_\sqrt{3}^\sqrt{6}{\sqrt{12-x^2}}\,dx&=\int_{\frac{\pi}{6}}^{\frac{\pi}{4}}{\sqrt{12-\left(2\sqrt{3}\sin{\theta}\right)^2}}\cdot 2\sqrt{3}\cos{\theta}\,d\theta\\[1.5ex]
&=12\int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\sqrt{1-\sin^2{\theta}}\cdot\cos{\theta}\,d\theta\\[1.5ex]
&=12\int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\cos^2{\theta}\,d\theta\,\,(\,\because 積分区間で\cos{\theta}>0より)\\[1.5ex]
&=12\int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\frac{1+\cos{2\theta}}{2}\,d\theta\\[1.5ex]
&=6\left[\theta+\frac{1}{2}\sin{2\theta}\right]_{\frac{\pi}{6}}^{\frac{\pi}{4}}\\[1.5ex]
&=6\left(\frac{\pi}{4}+\frac{1}{2}-\frac{\pi}{6}-\frac{\sqrt{3}}{4}\right)\\[1.5ex]
&=\frac{\pi}{2}+3-\frac{3\sqrt{3}}{2}
\end{align}
$$と計算できる.
3つ目の積分は,
$$
\int_\sqrt{3}^\sqrt{6}{x}\,dx=\left[\frac{x^2}{2}\right]_\sqrt{3}^\sqrt{6}=\frac{3}{2}
$$となる.
よって,
$$
\begin{align}
S&=\left(\sqrt{3}-\frac{4}{3}\right)+\left(\frac{\pi}{2}+3-\frac{3\sqrt{3}}{2}\right)-\left(\frac{3}{2}\right)\\[1.5ex]
&=\frac{\pi}{2}-\frac{\sqrt{3}}{2}+\frac{1}{6}
\end{align}
$$となる.
やはり, 何も考えずゴリゴリに積分計算で求まる理系の解法の方が楽ですね.
youtubeでも解説しています.